Question

【题目】已知椭圆 的右顶点为 ，离心率为 ．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设过右焦点F且斜率不为0的动直线l与椭圆交于M，N两点，过M作直线x=a2的垂线，垂足为M1 ， 求证：直线M1N过定点，并求出定点．

Answer 1

【答案】解：（Ⅰ）由题意可得： ，离心率 ，所以椭圆C的方程为 ．…

（Ⅱ）方法1：右焦点为F（1，0），因为直线l的斜率不为0，所以可设直线方程为x=ty+1，将其代入x2+2y2﹣2=0，并化简得：t2y2+2ty﹣1=0，

设M（x1，y1），N（x2，y2），M1（2，y1）由韦达定理得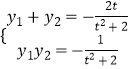： ，即y1+y2=2ty1y2直线M1N的方程为 ，令y=0，则有 = ，

因此直线l恒过定点 …

方法2：右焦点为F（1，0），因为直线l的斜率不为0，所以可设直线方程为x=my+1，将其代入x2+2y2﹣2=0，并化简得：（m2+2）y2+2my﹣1=0，不妨设y1＜y2，解得： 设M（x1，y1），N（x2，y2），则M1（2，y1），所以直线M1N的方程为 ，

当y=0时 = ．

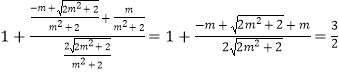当y1＞y2时，同理可得直线过定点 ．

综上所述，直线l过定点，且该定点为 …．

【解析】（1）根据题意，即可求出椭圆方程中的a，b，c，（2）方法1：右焦点为F（1，0），设直线方程为x=ty+1，将其代入x2+2y2﹣2=0，并化简得：t2y2+2ty﹣1=0，设M（x1，y1），N（x2，y2），M1（2，y1）由韦达定理得出直线M1N的方程，可得出该直线方程过定点（,0），方法2：右焦点为F（1，0），因为直线l的斜率不为0，所以可设直线方程为x=my+1，将其代入x2+2y2﹣2=0，并化简得：（m2+2）y2+2my﹣1=0，不妨设y1＜y2，根据求根公式求得y1，y2，根据两点式表示出直线M1N的方程，当y=0时，可得到x=，即该直线方程过定点（,0）.