题目内容

证明下列不等式．
（1）求证：当a、b、c为正数时，（a+b+c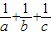）（）≥9．
（2）已知n≥0，试用分析法证明：．
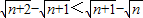【答案】分析：（1）将不等式左边展开，根据a、b、c为正数，利用基本不等式可证得（a+b+c）（）≥9成立；
（2）移项将不等式化为，两边平方整理后，可得，比较（n+1）2与n2+2n的大小可得答案．
解答：证明：（1）左边=
因为：a、b、c为正数
所以：左边=3+2+2+2=9
∴（a+b+c）（）≥9
（2）要证成立，
需证
需证
需证
需证（n+1）2＞n2+2n
需证n2+2n+1＞n2+2n，
只需证1＞0
因为1＞0显然成立，所以原命题成立
点评：本题考查的知识点是不等式的证明，其中（1）考查的知识点是基本不等式，（2）考查的知识点是分析法证明．
练习册系列答案
相关题目
证明下列不等式：
（1）a，b都是正数，且a+b=1，求证：(1+
1
a
)(1+
1
b
)≥9；
（2）设实数x，y满足y+x2=0，且0＜a＜1，求证：loga(ax+ay)＜
1
8
+loga2．
证明下列不等式．
（1）求证：当a、b、c为正数时，（a+b+c）（
1
a
+
1
b
+
1
c
）≥9．
（2）已知n≥0，试用分析法证明：
n+2
-
n+1
＜
n+1
-
n
．
证明下列不等式：
（1）对任意的正实数a，b，有
1
1+a
≥
1
1+b
-
a-b
(1+b)2
；
（2）
C
0
n
•
50
50+1
+
C
1
n
•
51
51+1
+
C
2
n
•
52
52+1
+…+
C
n
n
•
5n
5n+1
≥
2n•5n
3n+5n
，n∈N．
（2011•太原模拟）证明下列不等式：
（1）用分析法证明：
3
+
8
＞1+
10
；
（2）已知a，b，c是不全相等的正数，证明a2+b2+c2＞ab+bc+ca．
证明下列不等式：
（1）若x，y，z∈R，a，b，c∈R+，则
b+c
a
x2+
c+a
b
y2+
a+b
c
z2≥2（xy+yz+zx）
（2）若x，y，z∈R+，且x+y+z=xyz，则
y+z
x
+
z+x
y
+
x+y
z
≥2（
1
x
+
1
y
+
1
z
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网