题目内容
10.已知a>0且a≠1.设命题p:函数y=ax是定义在R上的增函数;命题q:?x∈R,使方程x2+ax+1<0成立.若“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.分析 若“p或q”为真命题,“p且q”为假命题,则命题p,q一真一假,进而可得实数a的取值范围.
解答 解:若函数y=ax是定义在R上的增函数,
则a>1,
即命题p:a>1,
若?x∈R,使方程x2+ax+1<0成立.
则△=a2-4>0,
结合a>0且a≠1得:a>2,
即命题q:a>2,
若“p或q”为真命题,“p且q”为假命题,则命题p,q一真一假,
p真q假时,1<a≤2,
p假q真时,不存在满足条件的a值,
综上可得:1<a≤2.
点评 本题以命题的真假判断与应用为载体,主要考查逻辑联结词,指数函数的单调性,二次函数的图象和性质.

练习册系列答案
相关题目
1.设向量$\overrightarrow{a}$=(λ,λ-2),$\overrightarrow{b}$=(1,2),若(2$\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$),则λ=( )
| A. | -1或$-\frac{7}{4}$ | B. | -1或$\frac{7}{4}$ | C. | 1或-$\frac{7}{4}$ | D. | 1或$\frac{7}{4}$ |
2.关于x的方程(m+3)x2-4mx+2m-1=0的两根异号,且负根的绝对值比正根大,那么实数m的取值范围为( )
| A. | (-3,0) | B. | (0,3) | C. | (-∞,-3)∪(0,+∞) | D. | (-∞,0)∪(3,+∞) |
19.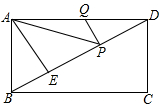 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
则AP+PQ的最小值为( )
 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,则AP+PQ的最小值为( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
20.平面向量$\overrightarrow{a}$,$\overrightarrow{b}$共线的充要条件是( )
| A. | $\overrightarrow{a}$,$\overrightarrow{b}$方向相同 | |
| B. | $\overrightarrow{a}$,$\overrightarrow{b}$两向量中至少有一个为零向量 | |
| C. | ?λ∈R,$\overrightarrow{b}$=λ$\overrightarrow{a}$ | |
| D. | 存在不全为零的实数λ1,λ2,λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$=$\overrightarrow{0}$ |
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD