题目内容
20.平面向量$\overrightarrow{a}$,$\overrightarrow{b}$共线的充要条件是( )| A. | $\overrightarrow{a}$,$\overrightarrow{b}$方向相同 | |
| B. | $\overrightarrow{a}$,$\overrightarrow{b}$两向量中至少有一个为零向量 | |
| C. | ?λ∈R,$\overrightarrow{b}$=λ$\overrightarrow{a}$ | |
| D. | 存在不全为零的实数λ1,λ2,λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$=$\overrightarrow{0}$ |
分析 分别对A、B、C、D各个选项判断即可.
解答 解:对于A:$\overrightarrow{a}$,$\overrightarrow{b}$共线不一定同向;
对于B:$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量也可以共线;
对于C:当$\overrightarrow{a}$=$\overrightarrow{0}$,$\overrightarrow{b}$≠$\overrightarrow{0}$时$\overrightarrow{b}$=λ$\overrightarrow{a}$不成立,
故选:D.
点评 本题给出两个向量$\overrightarrow{a}$、$\overrightarrow{b}$,叫我们探求$\overrightarrow{a}$、$\overrightarrow{b}$共线的充要条件,着重考查了零向量的性质和数乘向量的定义等知识,属于基础题.

练习册系列答案
相关题目
5.f(x)是定义在R上图形关于y轴对称,且在[0,+∞)上是减函数,下列不等式一定成立的是( )
| A. | f[${\frac{2}{{2-{a^2}}}}$]<f(${{a^2}-2a+\frac{5}{4}}$) | B. | f[-cos60°]<f(tan30°) | ||
| C. | f[-(cos60°)2]≥f(${{a^2}-2a+\frac{5}{4}}$) | D. | f[-sin45°]>f(-3a+2) |
9.已知函数f(x)的定义域为R,则命题p:“函数f(x)为奇函数”是命题q:“?x0∈R,f(x0)=-f(-x0)”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
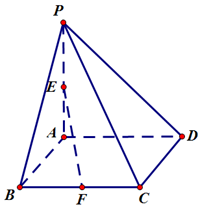 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.