题目内容
如图,已 知四棱锥
知四棱锥 的底面为直角梯形,AD∥BC,∠BCD=90°
的底面为直角梯形,AD∥BC,∠BCD=90° ,PA=PB,PC=PD
,PA=PB,PC=PD
(1)证明:平面 平面ABCD;
平面ABCD;
(2)如果
 ,且侧面
,且侧面 的面积为8,求四棱锥
的面积为8,求四棱锥 的体积。
的体积。
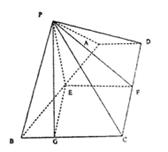
(1)解:取AB、CD 的中点E、F。连结PE、EF、PF,
由PA=PB、PC=PD得PE⊥AB,PF⊥CD  EF为直角梯形的中位线,
EF为直角梯形的中位线,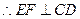
又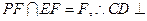 平面
平面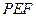
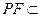 平面
平面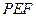 ,得
,得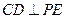
又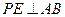 且梯形两腰AB、CD必交
且梯形两腰AB、CD必交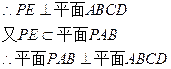
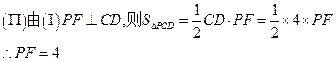
由已知,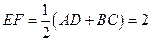 又在直角
又在直角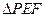 中,
中,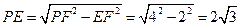 即四棱锥
即四棱锥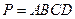 的高为
的高为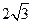
四棱锥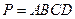 的体积
的体积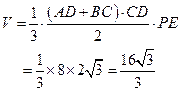
解析

练习册系列答案
相关题目
 (本题满分12分) 如图:已知四棱锥
(本题满分12分) 如图:已知四棱锥
 的底面是正方形,
的底面是正方形, ,且
,且 ,点
,点 分别在侧棱
分别在侧棱 、
、 上,且
上,且 。
。
 ;
; ,求平面
,求平面 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值. 的底面是正方形,
的底面是正方形, ⊥底面
⊥底面 ,且
,且 ,点
,点 、
、 分别为侧棱
分别为侧棱 、
、 的中点
的中点 
 ∥平面
∥平面 ;
; ⊥平面
⊥平面 .
. 的底面为矩形,
的底面为矩形, 且
且 平面
平面 分别为
分别为 的中点.
的中点.
 ;
; 的大小值.
的大小值.