题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{2x-10,x≤7}\\{\frac{1}{f(x-2)},x>7}\end{array}\right.$,若an=f(n)(n∈N*),则数列{an}的前50项和等于$\frac{225}{4}$.分析 n≤7时,an=f(n)=2n-10,可得a6=f(6),a7=f(7).x>7时,a8=f(8)=$\frac{1}{f(6)}$,a9=f(9)=$\frac{1}{f(7)}$,n≥10时,an=f(n)=$\frac{1}{f(n-2)}$=f(n-4).即可得出.
解答 解:n≤7时,an=f(n)=2n-10,
∴a6=f(6)=2×6-10=2,a7=f(7)=2×7-10=4.
n>7时,a8=f(8)=$\frac{1}{f(6)}$=$\frac{1}{2}$,a9=f(9)=$\frac{1}{f(7)}$=$\frac{1}{4}$,a10=f(10)=$\frac{1}{f(8)}$=f(6)=2,a11=f(11)=$\frac{1}{f(9)}$=f(7)=4,
a12=f(12)=$\frac{1}{f(10)}$=f(8)=$\frac{1}{2}$,…,n≥10时,an=f(n)=$\frac{1}{f(n-2)}$=f(n-4).
∴数列{an}的前50项和为:$\frac{6×(-8+2)}{2}$+11×$(4+\frac{1}{2}+\frac{1}{4}+2)$=$\frac{225}{4}$.
故答案为:$\frac{225}{4}$.
点评 本题考查了数列递推关系、数列的周期性、等差数列的通项公式与求和公式、分段函数的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.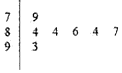 如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
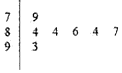 如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )| A. | 85.84 | B. | 84.85 | C. | 85.87 | D. | 84.86 |
17.已知{an}是等差数列,a1=-26,a8+a13=5,当{an}的前n项和Sn取最小值时,n等于( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
7.p:m>-3,q:方程$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{m-1}$=1表示的曲线是椭圆,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |