题目内容
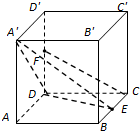 在边长为2的正方体ABCD-A'B'C'D'中,E是BC的中点,F是DD'的中点
在边长为2的正方体ABCD-A'B'C'D'中,E是BC的中点,F是DD'的中点(1)求证:CF∥平面A'DE
(2)求二面角E-A'D-A的平面角的余弦值.
分析:(1)分别以DA,DC,DD'为x轴,y轴,z轴建立空间直角坐标系,求出各顶点坐标后,进而求出直线CF的方向向量和平面A'DE的法向量,根据两个向量的数量积为0,得到两个向量垂直后,进而得到CF∥平面A'DE
(2)结合正方体的几何特征,可得
=(0,2,0)是面AA'D的法向量,结合(1)中平面A'DE的法向量为
=(-2,1,2),代入向量夹角公式,即可求出二面角E-A'D-A的平面角的余弦值.
(2)结合正方体的几何特征,可得
| DC |
| n |
解答:证明(1):分别以DA,DC,DD'为x轴,y轴,z轴
建立空间直角坐标系,
则A'(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),…(2分)
则
=(2,0,2),
=(1,2,0),
设平面A'DE的法向量是
=(a,b,c),
则
,取
=(-2,1,2),…(4分)
=(0,-2,1),∵
•
=-2+2=0,∴
⊥
,
所以,CF∥平面A'DE.…(6分)
解:(2)由正方体的几何特征可得
=(0,2,0)是面AA'D的法向量
又由(1)中向量
=(-2,1,2)为平面A'DE的法向量
故二面角E-A'D-A的平面角θ满足;
cosθ=
=
即二面角E-A'D-A的平面角的余弦值为
…(8分)
建立空间直角坐标系,
则A'(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),…(2分)
则
| DA′ |
| DE |
设平面A'DE的法向量是
| n |
则
|
| n |
| CF |
| CF |
| n |
| CF |
| n |
所以,CF∥平面A'DE.…(6分)
解:(2)由正方体的几何特征可得
| DC |
又由(1)中向量
| n |
故二面角E-A'D-A的平面角θ满足;
cosθ=
| ||||
|
|
| 1 |
| 3 |
即二面角E-A'D-A的平面角的余弦值为
| 1 |
| 3 |
点评:本题考查的知识点是用空间向量求平面间的夹角,向量语言表述线面的平行关系,其中建立适当的空间直角坐标系,将空间线面关系及面面夹角转化为向量夹角问题,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
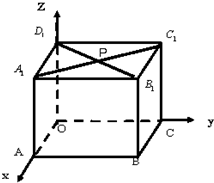 (1)如图所示,在边长为2的正方体OABC-A1B1C1D1中,A1C1交B1D1于P.分别写出O、A、B、C、A1、B1、C1、D1、P的坐标.
(1)如图所示,在边长为2的正方体OABC-A1B1C1D1中,A1C1交B1D1于P.分别写出O、A、B、C、A1、B1、C1、D1、P的坐标.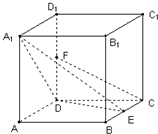 在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,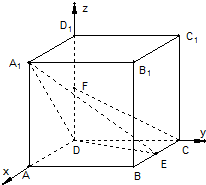 在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.