题目内容
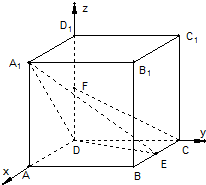 在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.(1)求证:CF∥平面A1DE;
(2)求点A到平面A1DE的距离.
分析:先分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角坐标系,则A(2,0,0),A1(2,0,2),E(1,2,0),D(0,0,0),C(0,2,0),F(0,0,1),再写出向量
,
的坐标,求出平面A1DE的法向量
.
(1)利用向量坐标之间的关系证得
⊥
,从而得出CF∥平面A1DE.
(2)利用向量的点到平面的距离公式即可求得点A到平面A1DE的距离.
| DA 1 |
| DE |
| n |
(1)利用向量坐标之间的关系证得
| CF |
| n |
(2)利用向量的点到平面的距离公式即可求得点A到平面A1DE的距离.
解答: 解 分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角
解 分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角
坐标系,则A(2,0,0),A1(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),则
=(2,0,2),
=(1,2,0)
设平面A1DE的法向量是
=(a,b,c)
则
,
=(-2,1,2)
(1)
=(0,-2,1),
∴
•
=-2+2=0,∴
⊥
,
所以,CF∥平面A1DE.
(2)点A到平面A1DE的距离是
d=
=
.
点A到平面A1DE的距离
.
 解 分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角
解 分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角坐标系,则A(2,0,0),A1(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),则
| DA 1 |
| DE |
设平面A1DE的法向量是
| n |
则
|
| n |
(1)
| CF |
∴
| CF |
| n |
| CF |
| n |
所以,CF∥平面A1DE.
(2)点A到平面A1DE的距离是
d=
|
| ||||
|
|
| 4 |
| 3 |
点A到平面A1DE的距离
| 4 |
| 3 |
点评:本小题主要考查点、线、面间的距离计算、直线与平面平行的判定等基础知识,考查运算求解能力,考查空间想象能力.属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
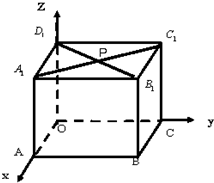 (1)如图所示,在边长为2的正方体OABC-A1B1C1D1中,A1C1交B1D1于P.分别写出O、A、B、C、A1、B1、C1、D1、P的坐标.
(1)如图所示,在边长为2的正方体OABC-A1B1C1D1中,A1C1交B1D1于P.分别写出O、A、B、C、A1、B1、C1、D1、P的坐标.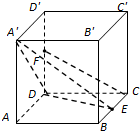 在边长为2的正方体ABCD-A'B'C'D'中,E是BC的中点,F是DD'的中点
在边长为2的正方体ABCD-A'B'C'D'中,E是BC的中点,F是DD'的中点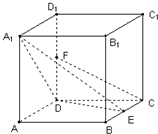 在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,