Question

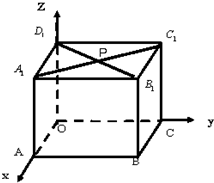（1）如图所示，在边长为2的正方体OABC-A₁B₁C₁D₁中，A₁C₁交B₁D₁于P．分别写出O、A、B、C、A₁、B₁、C₁、D₁、P的坐标．
（2）在空间直角坐标系中，A（2，3，5）、B（4，1，3），求A，B的中点P的坐标及A，B间的距离|AB|．

Answer 1

分析：（1）由已知中正方体ABCD-A₁B₁C₁D₁的棱长为2，P是正方形A₁B₁C₁D₁的中心点，易得到O、A、B、C、A₁、B₁、C₁、D₁、P的坐标；
（2）根据已知中，A，B两点的坐标，代入中点坐标公式和两点之间的距离公式，可得答案．

解答：解：（1）∵正方体ABCD-A₁B₁C₁D₁的棱长为2
又∵P是正方形A₁B₁C₁D₁的中心点，
∴O（0，0，0），A（2，0，0），B（2，2，0），C（0，2，0）
A₁（2，0，2），B₁（2，2，2），C₁（0，2，2），D₁（0，2，2），P（1，1，2）
（2）∵A（2，3，5）、B（4，1，3），
∴A，B的中点P的坐标为（3，2，4）
∴|AB|=

(2-4)2+(3-1)2+(5-3)2

=2

3

点评：本题考查的知识点是空间两点之间的距离，空间点的坐标表示，中点公式，难度不大，属于基础题．