题目内容
19．已知2sinθ-cosθ=1，3cosθ-2sinθ=a，记数a形成的集合为A，若x∈A，y∈A，则以点P（x，y）为顶点的平面图形可以是．| A． | 正方形 | B． | 五边形 | C． | 三角形 | D． | 线段 |
分析 由已知及同角的三角函数基本关系式的应用可解得sinθ，cosθ的值，即可解得集合A，在坐标系中即可得解．
解答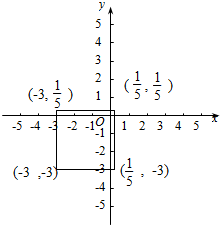 
解：由2sinθ-cosθ=1及sin2θ+cos2θ=1，
可以解得sinθ=0，cosθ=-1或sinθ=$\frac{4}{5}$，cos=$\frac{3}{5}$，
从而可以知道a=-3或$\frac{1}{5}$，所以A={-3，$\frac{1}{5}$}，
因为θ属于A，y属于A，所以P点的坐标可以是（-3，-3）或（$\frac{1}{5}$，$\frac{1}{5}$）或（-3，$\frac{1}{5}$）或（$\frac{1}{5}$，-3）四个点，
将这些坐标在直角坐标系中表示出来即可发现，这是一个正方形．
故选：A．
点评 本题主要考查了同角的三角函数基本关系式的应用，考查了集合的相关知识，属于基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
9．设定义域为R的函数f（x）满足$f（x+1）=\frac{1}{2}+\sqrt{f（x）-{{[f（x）]}^2}}$，且$f（-1）=\frac{1}{2}$，则f（2016）的值为（ ）
| A． | $\frac{1}{2}$ | B． | -1 | C． | 1 | D． | 2016 |
如图所示，?ABCD中，E、F分别是BC、DC的中点，BF与DE交于点G，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$．