题目内容
已知点P（-8，0）和圆C：x2+y2-2x+10y+4=0，
（1）求经过点P被圆C截得的线段最长的直线l的方程；
（2）过P点向圆C引割线，求被此圆截得的弦的中点的轨迹．
（1）求经过点P被圆C截得的线段最长的直线l的方程；
（2）过P点向圆C引割线，求被此圆截得的弦的中点的轨迹．
分析：（1）由题意可得经过点P被圆C截得的线段最长的直线l经过圆C的圆心，由两点式可得方程；
（2）利用垂径定理，可得勾股定理，从而可得方程，化简即可得出结论．
（2）利用垂径定理，可得勾股定理，从而可得方程，化简即可得出结论．
解答：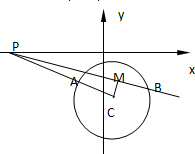
解：（1）化圆的方程为：（x-1）2+（y+5）2=22，圆心坐标：C（1，-5）．
由题意可得经过点P被圆C截得的线段最长的直线l经过圆C的圆心，
由两点式方程得：
=
，
化简得：5x+9y+40=0，
∴直线l的方程是：5x+9y+40=0…（6分）
（2）设中点M（x，y），则
∵CM⊥PM，∴△PCM是Rt△，
∴有：|PM|2+|MC|2=|PC|2
即：（x+8）2+y2+（x-1）2+（y+5）2=106，
化简得：x2+7x+y2+5y-8=0
故中点M的轨迹是圆x2+7x+y2+5y-8=0在圆C内部的一段弧 …（12分）
解：（1）化圆的方程为：（x-1）2+（y+5）2=22，圆心坐标：C（1，-5）．由题意可得经过点P被圆C截得的线段最长的直线l经过圆C的圆心，
由两点式方程得：
| y-0 |
| -5-0 |
| x+8 |
| 1+8 |
化简得：5x+9y+40=0，
∴直线l的方程是：5x+9y+40=0…（6分）
（2）设中点M（x，y），则
∵CM⊥PM，∴△PCM是Rt△，
∴有：|PM|2+|MC|2=|PC|2
即：（x+8）2+y2+（x-1）2+（y+5）2=106，
化简得：x2+7x+y2+5y-8=0
故中点M的轨迹是圆x2+7x+y2+5y-8=0在圆C内部的一段弧 …（12分）
点评：本题考查直线方程，看V轨迹方程，考查垂径定理，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目