题目内容
7.若空间向量$\overrightarrow a=(1,2,3)$,$\overrightarrow b=(x+y,y+z,z+x)$满足$(\overrightarrow a+\overrightarrow b)∥\overrightarrow b$,则一定有( )| A. | x=0 | B. | y=0 | C. | z=0 | D. | $\overrightarrow b=\overrightarrow 0$ |
分析 求出向量$\overrightarrow{a}+\overrightarrow{b}$,然后利用的共线可得$\frac{1}{x+y}=\frac{2}{y+z}=\frac{3}{z+x}$,解之可得结果.
解答 解:∵向量$\overrightarrow a=(1,2,3)$,$\overrightarrow b=(x+y,y+z,z+x)$,$\overrightarrow{a}+\overrightarrow{b}$=(x+y+1,y+z+2,z+x+3),
满足$(\overrightarrow a+\overrightarrow b)∥\overrightarrow b$,∴$\frac{x+y+1}{x+y}=\frac{y+z+2}{y+z}=\frac{z+x+3}{z+x}$,
可得$\frac{1}{x+y}=\frac{2}{y+z}=\frac{3}{z+x}$,
解得y=0,
故选:B.
点评 本题考查共线向量的坐标运算,考查计算能力,属基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
15.观察下列的图形中小正方形的个数,则第6个图中有( )个小正方形,第n个图中有( )个小正方形( )
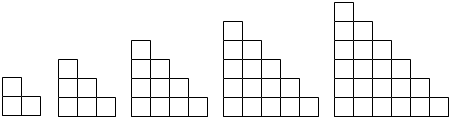

| A. | 28,$\frac{(n+1)(n+2)}{2}$ | B. | 14,$\frac{(n+1)(n+2)}{2}$ | C. | 28,$\frac{n}{2}$ | D. | 12,$\frac{{n}^{2}+n}{2}$ |
2.若复数Z=$\frac{a+3i}{1-2i}$(a∈R,i是虚数单位)是纯虚数,则在复平面内Z对应点的坐标为( )
| A. | (0,2) | B. | (0,3i ) | C. | (0,3) | D. | (0,2i) |
19.函数y=${log_{\frac{1}{2}}}$(3x-x2-2)的单调递减区间是( )
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,+∞) |
16.已知向量$\overrightarrow{a}$=(2,4),$\overrightarrow{b}$=(-1,1),则2$\overrightarrow{a}$+$\overrightarrow{b}$等于( )
| A. | (5,7) | B. | (5,9) | C. | (3,7) | D. | (3,9) |
