题目内容
16．已知向量$\overrightarrow{a}$=（2，4），$\overrightarrow{b}$=（-1，1），则2$\overrightarrow{a}$+$\overrightarrow{b}$等于（ ）| A． | （5，7） | B． | （5，9） | C． | （3，7） | D． | （3，9） |
分析 利用向量的坐标运算求解即可．
解答 解：向量$\overrightarrow{a}$=（2，4），$\overrightarrow{b}$=（-1，1），
则2$\overrightarrow{a}$+$\overrightarrow{b}$=（3，9）．
故选：D．
点评 本题考查向量的坐标运算，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
7．若空间向量$\overrightarrow a=（1，2，3）$，$\overrightarrow b=（x+y，y+z，z+x）$满足$（\overrightarrow a+\overrightarrow b）∥\overrightarrow b$，则一定有（ ）
| A． | x=0 | B． | y=0 | C． | z=0 | D． | $\overrightarrow b=\overrightarrow 0$ |
4．
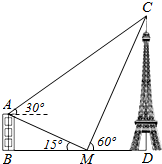如图，一栋建筑物AB的高为（30-10$\sqrt{3}$）m，在该建筑物的正东方向有一个通信塔CD，在它们之间的地面点M（B，M，D三点共线）处测得楼顶A，塔顶C的仰角分别是15°和60°，在楼顶A处测得塔顶C的仰角为30°，则通信塔CD的高为（ ）
如图，一栋建筑物AB的高为（30-10$\sqrt{3}$）m，在该建筑物的正东方向有一个通信塔CD，在它们之间的地面点M（B，M，D三点共线）处测得楼顶A，塔顶C的仰角分别是15°和60°，在楼顶A处测得塔顶C的仰角为30°，则通信塔CD的高为（ ）| A． | 30m | B． | 60m | C． | 30$\sqrt{3}$m | D． | 40$\sqrt{3}$m |
1．函数y=f（x）是R上的奇函数，当x＜0时，f（x）=2x，则当x＞0时，f（x）=（ ）
| A． | -2x | B． | 2-x | C． | -2-x | D． | 2x |
6．已知y=f（x）与y=f（x+1）都是定义在R上的偶函数，当x∈[-1，0]时，f（x）=-2x2-4x-2，若y=f（x）与g（x）=loga（x+1）的图象至少有3个交点，则a取值范围为（ ）
| A． | 0＜a＜$\frac{\sqrt{3}}{3}$ | B． | 0＜a＜$\frac{\sqrt{6}}{6}$ | C． | 1＜a＜$\sqrt{3}$ | D． | 1＜a＜$\sqrt{6}$ |