题目内容
15.观察下列的图形中小正方形的个数,则第6个图中有( )个小正方形,第n个图中有( )个小正方形( )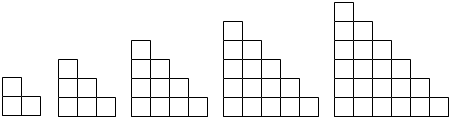
| A. | 28,$\frac{(n+1)(n+2)}{2}$ | B. | 14,$\frac{(n+1)(n+2)}{2}$ | C. | 28,$\frac{n}{2}$ | D. | 12,$\frac{{n}^{2}+n}{2}$ |
分析 由题意可得,f(1)=2+1,f(2)=3+2+1,f(3)=4+3+2+1,f(4)=5+4+3+2+1,f(5)=6+5+4+3+2+1,从而可得f(n),结合等差数列的求和公式可得.
解答 解:由题意可得,f(1)=2+1
f(2)=3+2+1
f(3)=4+3+2+1
f(4)=5+4+3+2+1
f(5)=6+5+4+3+2+1
…
f(n)=(n+1)+n+(n-1)+…+1=$\frac{(n+1)(n+2)}{2}$,
当n=6时,f(6)=28,
故选:A
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
3.由“正三角形的内切圆切于三边的中点”可类比猜想:正四面体的内切球切于四个面( )
| A. | 各正三角形内一点 | B. | 各正三角形的某高线上的点 | ||
| C. | 各正三角形的中心 | D. | 各正三角形外的某点 |
20.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{10}$的值的一个流程图,其中判断框内应填入的条件是( )
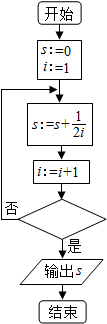

| A. | i>5 | B. | i<5 | C. | i>10 | D. | i<10 |
7.若空间向量$\overrightarrow a=(1,2,3)$,$\overrightarrow b=(x+y,y+z,z+x)$满足$(\overrightarrow a+\overrightarrow b)∥\overrightarrow b$,则一定有( )
| A. | x=0 | B. | y=0 | C. | z=0 | D. | $\overrightarrow b=\overrightarrow 0$ |
4.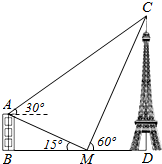 如图,一栋建筑物AB的高为(30-10$\sqrt{3}$)m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为( )
如图,一栋建筑物AB的高为(30-10$\sqrt{3}$)m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为( )
 如图,一栋建筑物AB的高为(30-10$\sqrt{3}$)m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为( )
如图,一栋建筑物AB的高为(30-10$\sqrt{3}$)m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为( )| A. | 30m | B. | 60m | C. | 30$\sqrt{3}$m | D. | 40$\sqrt{3}$m |