题目内容
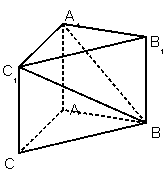
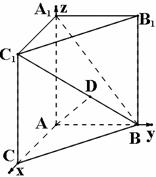
如图,在三棱柱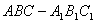 中,
中,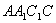 是边长为
是边长为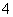 的正方形,平面
的正方形,平面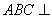 平面
平面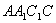 ,
,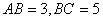 .
.
(1)求证: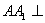 平面
平面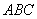 ;
;
(2)求二面角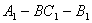 的余弦值;
的余弦值;
 (3)证明:在线段
(3)证明:在线段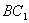 上存在点
上存在点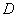 ,使得
,使得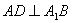 ,并求
,并求 的值。
的值。
解:(I)因为AA1C1C为正方形,所以AA1 ⊥AC.
因为平面ABC⊥平面AA1C1C,且AA1垂直于这两个平面的交线AC,
所以AA1⊥平面ABC.……… 3分
(II)由(I)知AA1 ⊥AC,AA1 ⊥AB. 由题知AB=3,BC=5,AC=4,所以AB⊥AC. 如图,以A为原点建立空间直角坐标系A-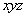 ,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
设平面A1BC1的法向量为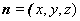 ,则
,则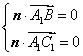 ,即
,即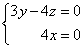 ,
,
令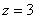 ,则
,则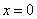 ,
,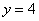 ,所以
,所以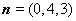 .……… 6分
.……… 6分
同理可得,平面BB1C1的法向量为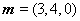 ,所以
,所以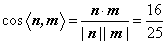 . 由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为
. 由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为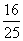 .……… 8分
.……… 8分
(III)设D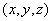 是直线BC1上一点,且
是直线BC1上一点,且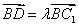 . 所以
. 所以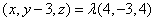 .解得
.解得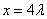 ,
,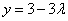 ,
,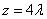 .
.
所以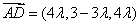 .
.
由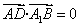 ,即
,即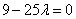 .解得
.解得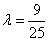 .……… 11分
.……… 11分
因为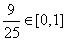 ,所以在线段BC1上存在点D,
,所以在线段BC1上存在点D,
使得AD⊥A1B.
 此时,
此时,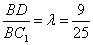 .……… 13分
.……… 13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在某种新型材料的研制中,实验人员获得了右边一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是
( )
|
| 1.99 | 3 | 4 | 5.1 | 6.12 |
|
| 1.5 | 4.04 | 7.5 | 12 | 18.01 |
A. 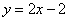 B.
B. 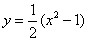
B.C.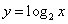 D.
D. 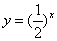
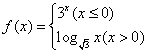 ,则
,则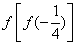 = .
= . ,则
,则 .
.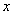
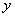
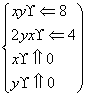 且z=5y-x的最大值为a,最小值为b,
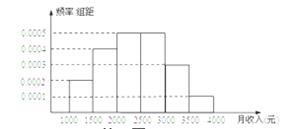
且z=5y-x的最大值为a,最小值为b,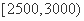 (元)月收入段应抽出
(元)月收入段应抽出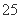 B.
B.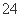 C.
C.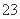 D.
D.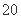
 ,
,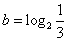 ,
, ,则( )
,则( )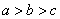 B.
B.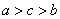 C.
C. D.
D.
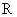 上的奇函数
上的奇函数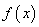 和定义在
和定义在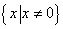 上的偶函数
上的偶函数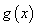 分别满足
分别满足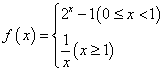 ,
,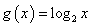 (
(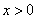 ),若存在实数
),若存在实数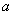 ,使得
,使得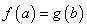 成立,则实数
成立,则实数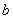 的取值范围是( )
的取值范围是( )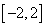 B.
B.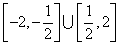 C.
C.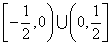 D.
D.