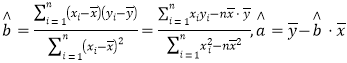题目内容
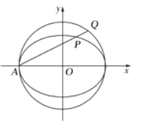
【题目】已知菱形ABCD的边长为2，∠BAD=120°，点E、F分别在边BC、DC上， 
=λ 
， 
=μ 
，若 
=1， 
=﹣ 
，则λ+μ=（ ）
A.
B.
C.
D.
【答案】C
【解析】解：由题意可得若 
=（ 
+ 
）（ 
+ 
）= 
+ 
+ 
+ 
=2×2×cos120°+ 
+λ +λ μ =﹣2+4μ+4λ+λμ×2×2×cos120°
=4λ+4μ﹣2λμ﹣2=1，
∴4λ+4μ﹣2λμ=3 ①．
=﹣ 
（﹣ 
）= 
=（1﹣λ） 
（1﹣μ） 
=（1﹣λ） （1﹣μ）
=（1﹣λ）（1﹣μ）×2×2×cos120°=（1﹣λ﹣μ+λμ）（﹣2）=﹣ 
，
即﹣λ﹣μ+λμ=﹣ 
②．
由①②求得λ+μ= 
，
故答案为： ．
利用两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义由 =1，求得4λ+4μ﹣2λμ=3 ①；再由 =﹣ ，求得﹣λ﹣μ+λμ=﹣ ②．结合①②求得λ+μ的值．
练习册系列答案
名校课堂系列答案
相关题目
【题目】禽流感一直在威胁我们的生活，某疾病控制中心为了研究禽流感病毒繁殖个数
（个）随时间
（天）变化的规律，收集数据如下：
天数 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散点图可看出样本点分布在一条指数型函数
的周围.
保留小数点后两位数的参考数据：
，
，
，
，
，
，
，
，其中
（1）求出关于的回归方程（保留小数点后两位数字）；
（2）已知
，估算第四天的残差.
参考公式：
