题目内容
在△ABC所在平面上有一点P,满足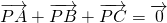 ,则△PBC与△ABC面积之比是
,则△PBC与△ABC面积之比是
- A.

- B.

- C.

- D.

A
分析:根据点所满足的条件知,P是三角形的重心,根据重心的特点,得到两个三角形的高之比,而两个三角形底边相同,所以得到结果.
解答:∵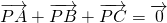 ,
,
∴P是三角形的重心,
∴P到顶点的距离是到对边距离的2倍,
∵△PBC与△ABC底边相同,
∴△PBC与△ABC面积之比是
故选A
点评:用一组向量来表示一个向量,是以后解题过程中常见到的,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,三角函数问题,本题把条件等式中的一个向量移项以后,就是用一组基底来表示向量.
分析:根据点所满足的条件知,P是三角形的重心,根据重心的特点,得到两个三角形的高之比,而两个三角形底边相同,所以得到结果.
解答:∵
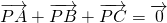 ,
,∴P是三角形的重心,
∴P到顶点的距离是到对边距离的2倍,
∵△PBC与△ABC底边相同,
∴△PBC与△ABC面积之比是

故选A
点评:用一组向量来表示一个向量,是以后解题过程中常见到的,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,三角函数问题,本题把条件等式中的一个向量移项以后,就是用一组基底来表示向量.

练习册系列答案
相关题目
 =
= +
+ +
+ ,且
,且 •
• =8,则边AC上的高h的最大值为________.
=8,则边AC上的高h的最大值为________. ,则点O是△ABC的( )
,则点O是△ABC的( ) =
= +
+ +
+ ,且
,且 •
• =8,则边AC上的高h的最大值为 .
=8,则边AC上的高h的最大值为 .