题目内容
若∠B=60°,O为△ABC的外心,点P在△ABC所在的平面上, =
= +
+ +
+ ,且
,且 •
• =8,则边AC上的高h的最大值为________.
=8,则边AC上的高h的最大值为________.

分析:根据题意,得点P是△ABC的垂心,从而
 •
• =0,将
=0,将 •
• 化简为
化简为 •
• =8,结合∠B=60°算出
=8,结合∠B=60°算出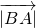 •
•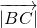 和三角形ABC的面积.利用余弦定理,算出当且仅当
和三角形ABC的面积.利用余弦定理,算出当且仅当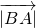 =
=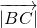 =4时,
=4时,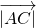 有最小值为4,结合三角形面积为4
有最小值为4,结合三角形面积为4 ,可得AC上的高h的最大值为2
,可得AC上的高h的最大值为2 .
.解答:
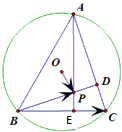 解:∵O为△ABC的外心,
解:∵O为△ABC的外心, =
= +
+ +
+ ,
,∴点P是△ABC的垂心,即P是三条高线的交点
∴
 •
• =(
=( +
+ )
) =8
=8∵
 •
• =0,∴
=0,∴ •
• =8
=8∵∠B=60°,∴
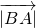 •
•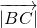 cos60°=8,得
cos60°=8,得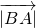 •
•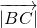 =16
=16根据正弦定理的面积公式,得S△ABC=

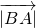 •
•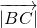 sin60°=4
sin60°=4
∵
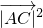 =
=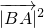 +
+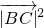 -2
-2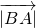 •
•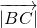 cos60°=
cos60°=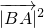 +
+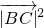 -16
-16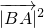 +
+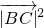 ≥2
≥2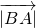 •
•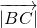 =32
=32∴
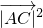 ≥16,得当且仅当
≥16,得当且仅当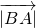 =
=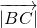 =4时,
=4时,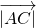 有最小值为4
有最小值为4∵S△ABC=

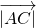 •h=4
•h=4 ,h是边AC上的高
,h是边AC上的高∴h≤
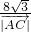 =2
=2 ,当且仅当
,当且仅当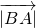 =
=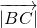 =
=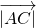 =4时,边AC上的高h的最大值为2
=4时,边AC上的高h的最大值为2
故答案为:2

点评:本题在△ABC中,已知一个角和两边长度之积,求另一边上高的最大值,着重考查了三角形外心与垂直的联系、平面向量数量积的运算性质和正余弦定理等知识,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知直线x=b交双曲线
-
=1(a>0,b<0)于A、B两点,O为坐标原点,若∠AOB=60°,则此双曲线的渐近线方程是( )
| y2 |
| a2 |
| x2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
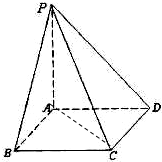 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,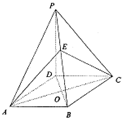 (2013•婺城区模拟)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.
(2013•婺城区模拟)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.