题目内容
如图,平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,若
,过A、B分别作两平面交线的垂线,垂足为A′、B′,若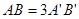 ,则AB与平面β所成的角的正弦值是( )
,则AB与平面β所成的角的正弦值是( )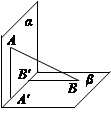
A.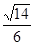 | B.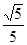 | C.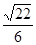 | D.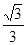 |
A
解析试题分析:
连接 ,
,
因为平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,所以
,过A、B分别作两平面交线的垂线,垂足为A′、B′,所以 是
是 与平面
与平面 所成的角,
所成的角,
设 ,因为
,因为 ,所以
,所以 ,
,
设 则
则 ,解得
,解得 ,
,
所以 ,
, ,
,
所以
考点:用空间向量求直线与平面的夹角.
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
若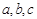 是空间三条不同的直线,
是空间三条不同的直线,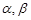 是空间两个不同的平面,则下列命题中,逆命题不正确的是( )
是空间两个不同的平面,则下列命题中,逆命题不正确的是( )
A.当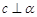 时,若 时,若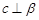 ,则 ,则 |
B.当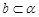 时,若 时,若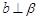 ,则 ,则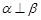 |
C.当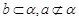 且 且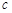 是 是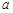 在 在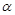 内的射影时,若 内的射影时,若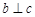 ,则 ,则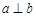 |
D.当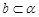 且 且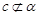 时,若 时,若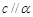 ,则 ,则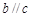 |
已知直线l,m和平面α, 则下列命题正确的是
A.若l∥m,m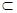 α,则l∥α α,则l∥α |
B.若l∥α,m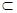 α,则l∥m α,则l∥m |
| C.若l⊥m,l⊥α,则m∥α |
D.若l⊥α,m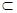 α,则l⊥m α,则l⊥m |
下列命题中,m、n表示两条不同的直线,α、β、γ表
示三个不同的平面.
①若m⊥α,n∥α,则m⊥n;
②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n;
④若α∥β,β∥γ,m⊥α,则m⊥γ.
则正确的命题是
| A.①③ | B.②③ | C.①④ | D.②④ |
在空间,下列命题正确的是( )
| A.平行直线在同一平面内的射影平行或重合 | B.垂直于同一平面的两条直线平行 |
| C.垂直于同一平面的两个平面平行 | D.平行于同一直线的两个平面平行 |
设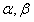 为两个平面,
为两个平面,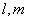 为两条直线,且
为两条直线,且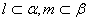 ,有如下两个命题:
,有如下两个命题:
①若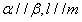 ;②若
;②若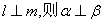 . 那么( )
. 那么( )
| A.①是真命题,②是假命题 | B.①是假命题,②是真命题 |
| C.①、②都是真命题 | D.①、②都是假命题 |
 是两个不同的平面,则下列四个命题中是真命题的是( )
是两个不同的平面,则下列四个命题中是真命题的是( )



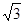 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).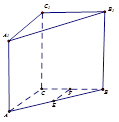
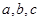 是三条不同的直线,
是三条不同的直线,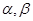 是两个不同的平面,在下列命题:
是两个不同的平面,在下列命题: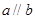 ,且
,且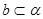 ,则
,则
 ,且
,且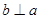 ,则
,则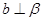
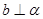 ,则
,则