题目内容

若函数f(x)=的值域为［-1，5］，求实数a、c.

解:由y=f(x)=，得x2y-ax+cy-1=0.当y=0时,ax=-1,∴a≠0.当y≠0时，

    ∵x∈R,∴Δ=a2-4y(cy-1)≥0.

    ∴4cy2-4y-a2≤0.∵-1≤y≤5,

    ∴-1、5是方程4cy2-4y-a2=0的两根.

    ∴

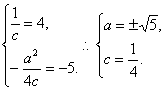
讲评:求f(x)=(a12+a22≠0)的值域时，常利用函数的定义域非空这一隐含的条件，将函数转化为方程，利用Δ≥0转化为关于函数值的不等式.求解时，要注意二次项系数为字母时要讨论.

练习册系列答案
相关题目
若函数f(x)=2x的反函数为f-1(x)，且f-1(a)+f-1(b)=4，则
1
a
+
1
b
的最小值是
 
．
已知
a
=(5
3
cosx，cosx)，
b
=(sinx，2cosx)，设函数f(x)=
a
•
b
+|
b
|2+
3
2
.
（Ⅰ）当x∈[
π
6
，
π
2
]，求函数f（x）的值域；
（Ⅱ）当x∈[
π
6
，
π
2
]时，若f（x）=8，求函数f(x-
π
12
)的值；
（Ⅲ）将函数y=f（x）的图象向右平移
π
12
个单位后，再将得到的图象上各点的纵坐标向下平移5个单位，得到函数y=g（x）的图象，求函数g（x）的表达式并判断奇偶性．
已知
a
=(5
3
cosx，cosx)，
b
=(sinx，2cosx)，设函数f(x)=
a
•
b
+|
b
|2+
3
2
．
（Ⅰ）当x∈[
π
6
，
π
2
]，求函数f（x）的值域；
（Ⅱ）当x∈[
π
6
，
π
2
]时，若f（x）=8，求函数f(x-
π
12
)的值．
若函数f(x)=-asincos(π-)的最大值为2，试确定常数a的值.

若函数f(x)=-1的定义域为R，则a的取值范围为__________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网