题目内容
5. 如图,在△ABC中,∠BAC=60°,AB=3,AC=2,D是BC边上的一点(含端点),则$\overrightarrow{AD}$•$\overrightarrow{BC}$的取值范围是[-6,1].
如图,在△ABC中,∠BAC=60°,AB=3,AC=2,D是BC边上的一点(含端点),则$\overrightarrow{AD}$•$\overrightarrow{BC}$的取值范围是[-6,1].
分析 建立平面直角坐标系,求出各点坐标,使用坐标计算.
解答 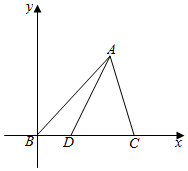 解:以BC所在直线为x轴,以B为原点建立平面直角坐标系,
解:以BC所在直线为x轴,以B为原点建立平面直角坐标系,
∵BC=$\sqrt{A{B}^{2}+A{C}^{2}-2AB•ACcos∠BAC}$=$\sqrt{7}$.∴cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•AC}$=$\frac{9+7-4}{6\sqrt{7}}$=$\frac{2}{\sqrt{7}}$.∴sinB=$\frac{\sqrt{3}}{\sqrt{7}}$.
∴A($\frac{6}{\sqrt{7}}$,$\frac{3\sqrt{3}}{\sqrt{7}}$),B(0,0),C($\sqrt{7}$,0).
设D(a,0),则$\overrightarrow{AD}$=(a-$\frac{6}{\sqrt{7}}$,-$\frac{3\sqrt{3}}{\sqrt{7}}$),$\overrightarrow{BC}$=($\sqrt{7}$,0).
∴$\overrightarrow{AD}•\overrightarrow{BC}$=$\sqrt{7}$a-6.
∵D是BC边上的一点(含端点),∴0≤a≤$\sqrt{7}$.
∴当a=0时,$\overrightarrow{AD}•\overrightarrow{BC}$取得最小值-6,当a=$\sqrt{7}$时,$\overrightarrow{AD}•\overrightarrow{BC}$取得最大值1.
故答案为[-6,1].
点评 本题考查了平面向量的数量积运算,建立坐标系是常用方法,属于中档题.

练习册系列答案
相关题目
16.已知函数f(x)=x2+$\frac{1}{2}$ax2+bx+c有两个极值点x1,x2,若f(x1)=x1<x2,则关于x的方程3(f(x))2+af(x)+b=0的不同实数的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.函数f(x)=lgx-sinx在(0,+∞)的零点个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.方程lnx+2x-6=0根的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.已知命题p:存在x∈R,使得ex>x,则¬p为( )
| A. | ¬p:存在x∈R,使得ex<x | B. | ¬p:任意x∈R,总有ex<x | ||
| C. | ¬p:存在x∈R,使得ex≤x | D. | ¬p:任意x∈R,总有ex≤x |
14.已知直线l过点P(3,4),它的倾斜角是直线y=x+1的两倍,则直线l的方程为( )
| A. | y-4=0 | B. | x-3=0 | C. | y-4=2(x-3) | D. | y-4=x-3 |
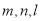 和三个平面
和三个平面 ,则下列命题中为假命题的是( )
,则下列命题中为假命题的是( )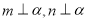 ,则
,则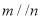
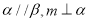 ,则
,则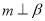
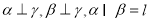 ,则
,则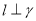
 ,则
,则