题目内容
数列{an}的奇数项成等差数列,偶数项成等比数列,公差与公比均为2,并且a2+a4=a1+a5,a4+a7=a6+a3.则使得am•am+1•am+2=am+am+1+am+2成立的所有正整数m的值为 .
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:首先,根据已知条件,求解该数列的前两项,然后,根据所给的等式确定m的值.
解答:
解:∵数列{an}的奇数项成等差数列,偶数项成等比数列,公差与公比均为2,
∴a3=a1+2,a5=a1+4,a7=a1+6,
a4=2a2,a6=4a2,
∵a2+a4=a1+a5,a4+a7=a6+a3
∴a2+2a2=a1+4+a1,2a2+6+a1=4a2+2+a1
∴a1=1,a2=2,
∵am•am+1•am+2=am+am+1+am+2成立,
∴由上面可以知数列{an}为:1,2,3,4,5,8,7,16,9,…
当m=1时等式成立,即 1+2+3=-6=1×2×3;等式成立.
当m=2时等式成立,即2×3×4≠2+3+4;等式不成立.
当m=3、4时等式不成立;
当m≥5时,
∵am•am+1•am+2为偶数,am+am+1+am+2为奇数,
∴可得m取其它值时,不成立,
∴m=1时成立.
故答案为:1
∴a3=a1+2,a5=a1+4,a7=a1+6,
a4=2a2,a6=4a2,
∵a2+a4=a1+a5,a4+a7=a6+a3
∴a2+2a2=a1+4+a1,2a2+6+a1=4a2+2+a1
∴a1=1,a2=2,
∵am•am+1•am+2=am+am+1+am+2成立,
∴由上面可以知数列{an}为:1,2,3,4,5,8,7,16,9,…
当m=1时等式成立,即 1+2+3=-6=1×2×3;等式成立.
当m=2时等式成立,即2×3×4≠2+3+4;等式不成立.
当m=3、4时等式不成立;
当m≥5时,
∵am•am+1•am+2为偶数,am+am+1+am+2为奇数,
∴可得m取其它值时,不成立,
∴m=1时成立.
故答案为:1
点评:本题重点考查了等差数列的概念和基本性质、等比数列的概念和基本性质等知识,属于中档题.解题关键是准确应用等差和等比数列的基本性质求解问题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
三个数a=0.22,b=log202,c=20.1之间的大小关系是( )
| A、a<c<b |
| B、a<b<c |
| C、b<a<c |
| D、b<c<a |
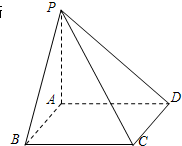 如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )
如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )| A、平面PAB⊥平面PAD |
| B、平面PAB⊥平面PBC |
| C、平面PBC⊥平面PCD |
| D、平面PCD⊥平面PAD |
若椭圆
+
=1的一个焦点和短轴的两端点构成一个正三角形,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示为函数f(x)=2sin(ωx+φ)(
如图所示为函数f(x)=2sin(ωx+φ)(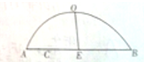 如图,A处为我军一炮兵阵地,距A处1000米的C处有一小山,山高为580米,在山的另一侧距C处3000米有敌武器库B,且A、B、C在同一水平直线删个,已知我炮兵轰击敌武器库是一段抛物线,这段抛物线的最大高度OE为800米.
如图,A处为我军一炮兵阵地,距A处1000米的C处有一小山,山高为580米,在山的另一侧距C处3000米有敌武器库B,且A、B、C在同一水平直线删个,已知我炮兵轰击敌武器库是一段抛物线,这段抛物线的最大高度OE为800米.