题目内容
已知|x-1|-|x+2|＞m恒成立，求m的取值范围．
考点：绝对值不等式
专题：函数的性质及应用
分析：根据绝对值函数的性质求出|x-1|-|x+2|的最小值即可得到结论
解答：
解：设f（x）=|x-1|-|x+2|，
若当x≥1时，f（x）=|x-1|-|x+2|=x-1-x-2=-3，
当-2＜x＜1时，f（x）=|x-1|-|x+2|=-x+1-x-2=-2x-1，
当x≤-2时，f（x）=|x-1|-|x+2|=-x+1+x+2=3，
即f(x)=
，
∴函数f（x）的最小值为-3，
∴要使|x-1|-|x+2|＞m恒成立，
则m≤-3．
若当x≥1时，f（x）=|x-1|-|x+2|=x-1-x-2=-3，
当-2＜x＜1时，f（x）=|x-1|-|x+2|=-x+1-x-2=-2x-1，
当x≤-2时，f（x）=|x-1|-|x+2|=-x+1+x+2=3，
即f(x)=
|
∴函数f（x）的最小值为-3，
∴要使|x-1|-|x+2|＞m恒成立，
则m≤-3．
点评：本题主要考查绝对值函数的性质，利用绝对值函数的特点构造函数，求出函数的最值是解决本题的关键．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
已知全集U=R，集合A={x|x2-x＞0}，B={x|lnx≤0}，则（∁UA）∩B=（ ）
| A、（0，1] |
| B、（-∞，0）∪（1，+∞） |
| C、∅ |
| D、（0，1） |
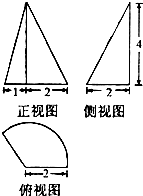
已知一个几何体的三视图（单位：cm）如图所示，求：某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|