题目内容
已知 ,其中向量
,其中向量 ,
, ,
, .在
.在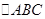 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 ,
, ,
, .
.
(1)如果三边 ,
, ,
, 依次成等比数列,试求角
依次成等比数列,试求角 的取值范围及此时函数
的取值范围及此时函数 的值域;
的值域;
(2) 在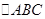 中,若
中,若 ,
,  ,求
,求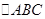 的面积.
的面积.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)先化简 ,然后根据三边关系结合余弦定理求得角
,然后根据三边关系结合余弦定理求得角 的取值范围,再将
的取值范围,再将 代入化简后的
代入化简后的 ,得到
,得到 ,根据三角函数在定区间上的值域求得函数
,根据三角函数在定区间上的值域求得函数 的值域;(2)根据题中所给信息
的值域;(2)根据题中所给信息 解得角
解得角 的大小,由
的大小,由 得到
得到 ,根据面积公式
,根据面积公式 ,求出面积.
,求出面积.
试题解析:(1)
 ,
,
2分
由已知 ,所以
,所以 ,
,
所以 ,
, ,则
,则 ,
,
故函数f(B)的值域为 ; 6分
; 6分
(2)由已知得 ,所以
,所以 , 8分
, 8分
所以 或
或 ,解得
,解得 或
或 (舍去), 10分
(舍去), 10分
由 ,得
,得 ,解得
,解得 ,
,
所以 . 12分
. 12分
考点:1、平面向量的数量积的运算;2、余弦定理;3、解三角形;4、等差数列的性质及应用;5、特殊角的三角函数值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, , 且
, 且
 的解析式;
的解析式; 时,
时,  的值.
的值. ,b=(
,b=(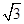 sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b. 上的最大值和最小值.
上的最大值和最小值. +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为
,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为 .
.
 的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由; 轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值. =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), |
| ;
; ,
, ,
, 为锐角.
为锐角. ,求
,求 的值;
的值; ,求
,求 的值.
的值. ,它们的夹角为
,它们的夹角为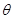 ,且
,且 ,
, ,
, 为正实数.
为正实数. 与
与 垂直,求
垂直,求 ;
; ,求
,求 的最小值及对应的
的最小值及对应的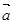 与
与 是否垂直?
是否垂直? 中,角
中,角 所对的边分别是
所对的边分别是 ,向量
,向量 ,向量
,向量 ,且
,且 .
. 的大小;
的大小; ,求
,求 .
. ,且x∈[0,
,且x∈[0, ],求
],求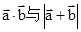 ;
; 的最小值是
的最小值是 ,求实数
,求实数 的值。
的值。