题目内容
已知 ,
, , 且
, 且
(1) 求函数 的解析式;
的解析式;
(2) 当 时,
时,  的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数 的最大值, 并求出相应的
的最大值, 并求出相应的 的值.
的值.
(1)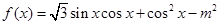 ;(2)
;(2)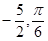 。
。
解析试题分析:(1)根据向量数量积的坐标运算可得 的解析式;(2)由(1)知
的解析式;(2)由(1)知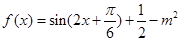
再由  求出
求出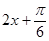 的范围,结合正弦函数的性质可求出
的范围,结合正弦函数的性质可求出 的最大值。
的最大值。
(1)
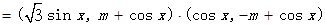
即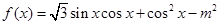 。
。
(2) 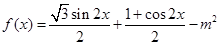
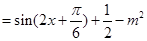
由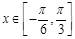 ,
, 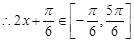 ,
, 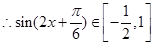 ,
,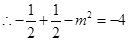 ,
, 
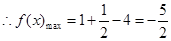 , 此时
, 此时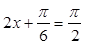 , 即
, 即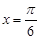 。
。
考点:(1)向量数量积的坐标运算;(2)二倍角正(余)弦公式的应用;(3)正弦函数的单调性。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 =(
=( sin x,sin x),
sin x,sin x),  ="(cos" x,sin x),x∈
="(cos" x,sin x),x∈ .
. ,求x的值;
,求x的值;  ,求
,求 的最大值.
的最大值.
 ,求
,求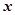 的值
的值 ,求
,求 的取值范围
的取值范围 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
 ,且
,且 ,求
,求 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角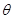 .
. ,
, ,
, ,
,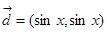 .
. 时,求向量
时,求向量 与
与 的夹角
的夹角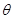 ;
;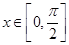 时,求
时,求 的最大值;
的最大值; ,将函数
,将函数 的图像向右平移
的图像向右平移 个长度单位,向上平移
个长度单位,向上平移 个长度单位
个长度单位 后得到函数
后得到函数 的图像,且
的图像,且 ,令
,令 ,求
,求 的最小值.
的最小值. 的离心率为
的离心率为 ,以椭圆
,以椭圆 的
的 为圆心作圆
为圆心作圆 ,设圆
,设圆 与点
与点 .
. 的最小值,并求此时圆
的最小值,并求此时圆 是椭圆
是椭圆 、
、 分别与
分别与 轴交于点
轴交于点 、
、 ,
, 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.
 在同一平面内,且
在同一平面内,且 .
.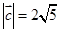 ,且
,且 ,求
,求 ;
; ,且
,且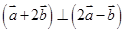 ,求
,求 与
与 的夹角.
的夹角. ,其中向量
,其中向量 ,
, ,
, .在
.在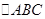 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 ,
, ,
, .
. 的取值范围及此时函数
的取值范围及此时函数 的值域;
的值域; ,
,  ,求
,求 的最小值是 。
的最小值是 。