题目内容

在△ABC中，
a
sinA
=
b
cosB
=
c
cosC
=2，则此三角形的面积为______．
∵
a
sinA
=
b
cosB
，
∴根据正弦定理
a
sinA
=
b
sinB
，可得cosB=sinB．
∵B∈（0，π），∴B=
π
4
．
同理可得C=
π
4
，得A=π-（A+B）=
π
2
．
∴△ABC是等腰直角三角形．
∵
a
sinA
=2，∴a=2sinA=2sin
π
2
=2．
由此可得b=c=
2
2
a=
2
，
∴此三角形的面积S=
1
2
bc=
1
2
×
2
×
2
=1．
故答案为：1
练习册系列答案
相关题目
（1）△ABC中，a=8,B=60°,C=75°,求b;
(2)△ABC中，B=30°,b=4,c=8,求C、A、a.
如图，隔河看两目标A、B，但不能到达，在岸边选取相距
3
km的C、D两点，并测得∠ACB=75°，∠BCD=45°，∠ADC=30°，∠ADB=45°（A、B、C、D在同一平面内），求两目标A、B之间的距离．
在△ABC中，AB=1，BC=2，则角C的取值范围是（　　）
A．(0，
π
6
]		B．(0，
π
6
]		C．(
π
6
，
π
2
]		D．[
π
6
，π)
设△ABC的三内角A、B、C的对边长分别为a、b、c，已知bcosC=（2a-c）cosB．
（Ⅰ）求角B的大小；
（Ⅱ）若x∈[0，π），求函数f（x）=sin（x-B）+sinx的值域．
在△ABC中，已知B=45°，D是BC上一点，AD=5，AC=7，DC=3，求AB的长．
在△ABC中，角A、B、C所对的边分别为a、b、c，已知
a
3
cosA
=
c
sinC
，
（Ⅰ）求A的大小；
（Ⅱ）若a=6，S=9
3
，求b和c的值．
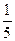如果一个等腰三角形的底边长是周长的，那么它的一个底角的余弦值为（  ）
A．B．C．D．
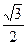
三角形ABC中，如果A=60º，C=45º，且a=,则c=        。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网