题目内容
如图,椭圆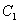 :
: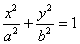 (
(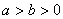 )和圆
)和圆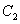 :
: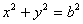 ,已知圆
,已知圆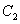 将椭圆
将椭圆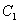 的长轴三等分,且
的长轴三等分,且 ,椭圆
,椭圆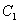 的下顶点为
的下顶点为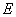 ,过坐标原点
,过坐标原点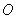 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线 与圆
与圆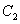 相交于点
相交于点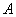 、
、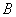 .
.
(Ⅰ )求椭圆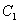 的方程;
的方程;
(Ⅱ)若直线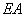 、
、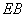 分别与椭圆
分别与椭圆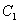 相交于另一个交点为点
相交于另一个交点为点 、
、 .
.
①求证:直线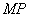 经过一定点;
经过一定点;
|
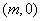 为圆心,
为圆心,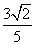 为半径的圆
为半径的圆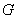 ,使得直线
,使得直线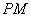 和直线
和直线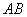 都与圆
都与圆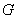 相交?若存在,请求出所有
相交?若存在,请求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 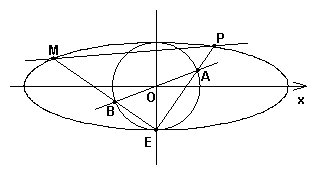
(Ⅰ )依题意,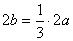 ,则
,则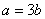 ,
,
∴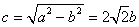 ,又
,又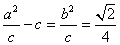 ,∴
,∴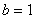 ,则
,则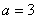 ,
,
∴椭圆方程为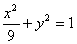 .
.
(Ⅱ)①由题意知直线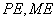 的斜率存在且不为0,设直线
的斜率存在且不为0,设直线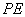 的斜率为
的斜率为 ,则
,则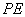 :
: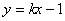 ,
,
由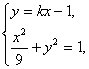 得
得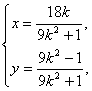 或
或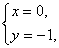
∴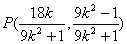 ,
,
用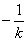 去代
去代 ,得
,得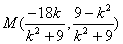 ,
,
方法1: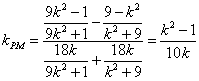 ,
,
∴ :
: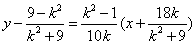 ,即
,即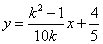 ,
,
∴直线 经过定点
经过定点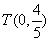 .
.
方法2:作直线 关于
关于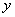 轴的对称直线
轴的对称直线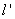 ,此时得到的点
,此时得到的点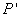 、
、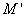 关于
关于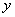 轴对称,则
轴对称,则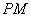 与
与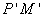 相交于
相交于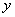 轴,可知定点在
轴,可知定点在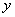 轴上,
轴上,
当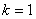 时,
时,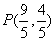 ,
,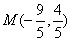 ,此时直线
,此时直线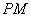 经过
经过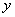 轴上的点
轴上的点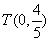 ,
,
∵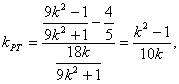
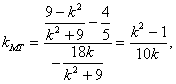
∴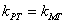 ,∴
,∴ 、
、 、
、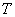 三点共线,即直线
三点共线,即直线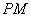 经过点
经过点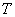 ,
,
综上所述,直线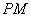 经过定点
经过定点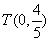 .
.
②由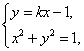 得
得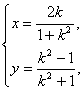 或
或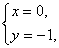 ∴
∴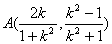 ,
,
则直线 :
: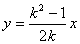 ,
,
设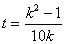 ,则
,则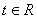 ,直线
,直线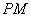 :
: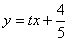 ,直线
,直线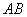 :
: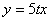 ,
,
假设存在圆心为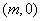 ,半径为
,半径为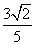 的圆
的圆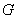 ,使得直线
,使得直线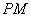 和直线
和直线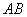 都与圆
都与圆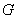 相交,
相交,
则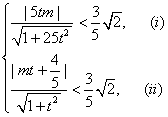 由(
由(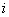 )得
)得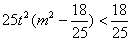 对
对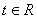 恒成立,则
恒成立,则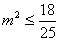 ,
,
由(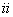 )得,
)得,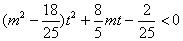 对
对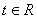 恒成立,
恒成立,
当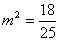 时,不合题意;当
时,不合题意;当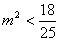 时,
时,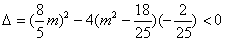 ,得
,得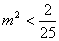 ,即
,即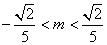 ,
,
∴存在圆心为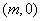 ,半径为
,半径为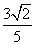 的圆
的圆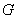 ,使得直线
,使得直线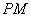 和直线
和直线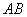 都与圆
都与圆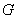 相交,所有
相交,所有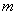 的取值集合为
的取值集合为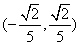 .
.
解法二:圆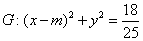 ,由上知
,由上知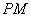 过定点
过定点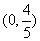 ,故
,故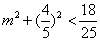 ;又直线
;又直线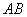 过原点,故
过原点,故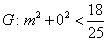 ,从而得
,从而得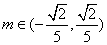 .
.

练习册系列答案
相关题目
在某学校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次.某同学在A处的命中率q1=0.25,在B处的命中率为q2.该同学选择先在A处投一球,以后都在B处投,用X表示该同学投篮训练结束后所得的总分,其分布列为
| X | 0 | 2 | 3 | 4 | 5 |
| P | 0.03 | p1 | p2 | p3 | p4 |
1)求 的值; 2)求随机变量X的数学期望EX;
的值; 2)求随机变量X的数学期望EX;
3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
 的首项为
的首项为 ,公差为
,公差为 ,且不等式
,且不等式 的解集为
的解集为 .
. ;
; ,求数列
,求数列 前
前 项和
项和 .
. 的离心率为
的离心率为 ,动
,动 是其内接三角形,且
是其内接三角形,且 .若AB的中点为D,D的轨迹E的离心率为
.若AB的中点为D,D的轨迹E的离心率为 ,则( )
,则( ) B.
B.  C.
C. D.
D. 
 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 ( )
( ) B
B  C
C  D
D 
 ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 
 ,
, 与
与 的夹角为60°,
的夹角为60°, ,且
,且 ,则k=( )
,则k=( ) B.
B. C.
C. D.
D.
 ,且是相互独立的,则灯泡甲亮的概率为( )
,且是相互独立的,则灯泡甲亮的概率为( ) B.
B. C.
C.
