题目内容
在正方形ABCD中，E，F分别为边AD，BC的中点，若沿EF将正方形折成一个二面角A-EF-D使得AD=
AE，则异面直线AD与CE所成角的余弦值为 ．
| 2 |
考点：异面直线及其所成的角
专题：空间角
分析：连结BE，CE、BC，由AD∥BC，得∠BCE是异面直线AD与CE所成角，由余弦定理得：cos∠BCE=
，由此能求出异面直线AD与CE所成角的余弦值．
| BC2+CE2-BE2 |
| 2BC•CE |
解答：
解：连结BE，CE、BC，
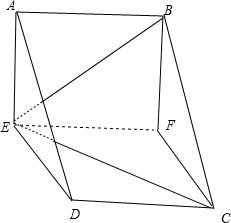设AE=x，则DE=x，AD=CB=
x，
∴AE2+DE2=AD2，∴AE⊥DE，
BE=CE=
=
x，
∵AD∥BC，∴∠BCE是异面直线AD与CE所成角，
由余弦定理得：
cos∠BCE=
=
=
．
故答案为：
．
设AE=x，则DE=x，AD=CB=| 2 |
∴AE2+DE2=AD2，∴AE⊥DE，
BE=CE=
| x2+4x2 |
| 5 |
∵AD∥BC，∴∠BCE是异面直线AD与CE所成角，
由余弦定理得：
cos∠BCE=
| BC2+CE2-BE2 |
| 2BC•CE |
=
| 2x2+5x2-5x2 | ||||
2×
|
=
| ||
| 10 |
故答案为：
| ||
| 10 |
点评：本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意余弦定理的合理运用．
练习册系列答案
相关题目
在△ABC中，若sin2A+sin2C+cos2B＜1，则△ABC一定是（ ）
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、不确定 |
如图，D是△ABC的边AB的中点，则向量
=（ ）
| CD |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
设数列{an}为公差为2的等差数列，记{an}的前n项和为Sn，令bn=Sn+an，若{bn}为递增数列，则a1的取值范围是（ ）
| A、（-4，+∞） |
| B、（-3，+∞） |
| C、（-2，+∞） |
| D、（0，+∞） |