题目内容
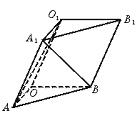
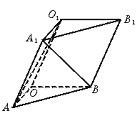
如图，三棱柱OAB—O1A1B1，平面OBB1O1⊥平面OAB，∠O1OB=60°,∠AOB=90°，且OB=OO1=2，OA=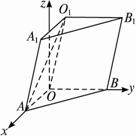
，求异面直线A1B与AO1所成角的大小.
解析：用平移A1B或AO1的方法求解，是很困难的，于是我们很自然想到向量法求解.充分利用∠AOB=90°，建立空间直角坐标系，写出有关点及向量的坐标，将几何问题转化为代数计算问题.?
建立如图所示的空间直角坐标系，则O（0，0，0），O1（0，1，
），A（，0，0），A1（
，1，
），B（0，2，0），?
∴
=（-
，1，-
），?
=（
，-1，
）.?
设异面直线所成的角为α，则cosα=
.?
故异面直线A1B与AO1所成角的大小为arccos
.
练习册系列答案
相关题目
（2002•上海）如图，三棱柱OAB-O1A1B1，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°，且OB=OO1=2，OA=
.
.
.求： 