题目内容
(本小题12分)已知椭圆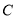 的两个焦点是
的两个焦点是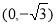 和
和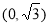 ,并且经过点
,并且经过点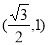 ,抛物线
,抛物线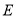 的顶点在坐标原点,焦点恰好是椭圆
的顶点在坐标原点,焦点恰好是椭圆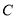 的右顶点
的右顶点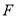 .
.
(1)求椭圆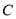 和抛物线
和抛物线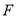 的标准方程;
的标准方程;
(2)过点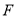 作两条斜率都存在且互相垂直的直线
作两条斜率都存在且互相垂直的直线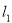 ,
,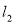 ,
, 交抛物线
交抛物线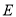 于点
于点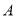 ,
,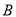 ,
, 交抛物线
交抛物线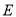 于点
于点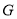 ,
, ,求
,求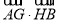 的最小值.
的最小值.
(1)椭圆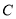 的标准方程为
的标准方程为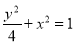 ,抛物线
,抛物线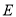 的标准方程为
的标准方程为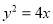 ;
;
(2) 有最小值
有最小值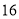 .
.
【解析】
试题分析:(1)由题意得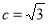 ,
,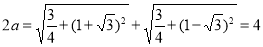 ,从而
,从而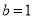 ,即可得椭圆
,即可得椭圆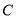 的标准方程为
的标准方程为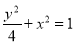 ,∴椭圆右顶点的坐标为
,∴椭圆右顶点的坐标为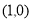 ,即抛物线的焦点坐标为
,即抛物线的焦点坐标为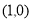 ,∴
,∴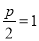 ,
,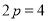 ,抛物线
,抛物线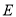 的标准方程为
的标准方程为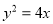 ;
;
(2)设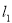 的方程:
的方程: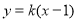 ,
,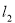 的方程:
的方程: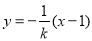 ,
,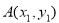 ,
,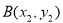 ,
,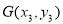 ,
,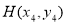 ,注意到
,注意到 ,且它们交于点
,且它们交于点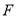 ,∴可将
,∴可将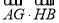 作如下变形:
作如下变形:
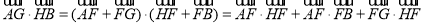
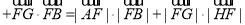 ,这样先将
,这样先将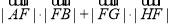 用
用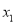 ,
,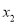 ,
,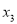 ,
,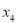 表示出来,再利用韦达定理用
表示出来,再利用韦达定理用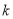 表示,再求其最小值.
表示,再求其最小值.
试题解析:(1)设椭圆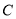 的标准方程为
的标准方程为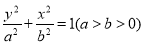 ,焦距为
,焦距为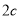 ,则由题意得
,则由题意得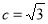 ,
,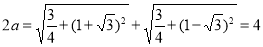 ,∴
,∴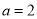 ,
,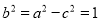 ,∴椭圆
,∴椭圆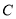 的标准方程为
的标准方程为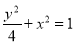 ,∴右顶点
,∴右顶点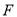 的坐标为
的坐标为 ,设抛物线
,设抛物线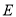 的标准方程为
的标准方程为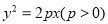 ,∴
,∴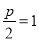 ,
, ,∴抛物线
,∴抛物线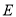 的标准方程为
的标准方程为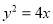 ;
;
(2)设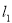 的方程:
的方程: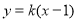 ,
,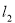 的方程:
的方程: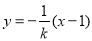 ,
,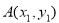 ,
,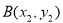 ,
,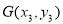 ,
,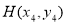 ,由
,由 ,消去
,消去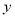 得:
得: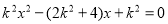 ,
,
∴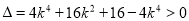 ,
,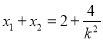 ,
,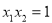 ,同理
,同理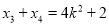 ,
,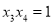 ,∴
,∴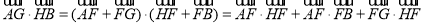
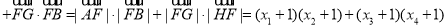
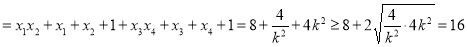 ,
,
当且仅当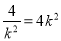 ,即
,即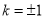 时,
时, 有最小值
有最小值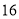 .
.
考点:1.椭圆的标准方程,抛物线的标准方程;2.平面向量的数量积;3.直线与抛物线的位置关系.
考点分析: 考点1:平面向量的数量积 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
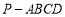 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,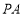 ⊥
⊥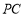 ,
,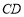 ⊥
⊥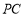 ,
, ,
,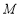 分别是
分别是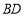 ,
,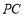 的中点,连结
的中点,连结 .求证:
.求证:
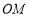 ∥平面
∥平面 ;
;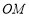 ⊥平面
⊥平面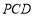 .
. ,
, ,则
,则 = .
= .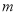 ,
,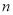 是两条不同直线,
是两条不同直线,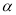 ,
, 是两个不同的平面,下列命题正确是是( )
是两个不同的平面,下列命题正确是是( ) ,
,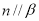 ,且
,且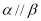 ,则
,则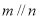
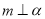 ,
,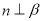 ,且
,且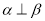 ,则
,则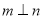
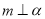 ,
,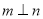 ,
,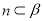 , 则
, 则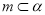 ,
,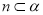 ,
,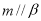 ,
,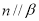 ,则
,则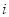 是虚数单位,复数
是虚数单位,复数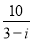 在复平面内表示的点在( )
在复平面内表示的点在( )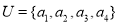 ,集合
,集合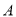 是集合
是集合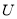 的恰有两个元素的子集,且满足下列三个条件:①若
的恰有两个元素的子集,且满足下列三个条件:①若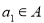 ,则
,则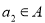 ;②若
;②若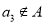 ,则
,则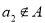 ;③若
;③若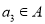 ,则
,则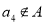 ,则集合
,则集合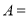 __________.(用列举法表示)
__________.(用列举法表示)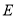 ,
,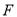 分别是正方体
分别是正方体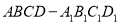 的棱
的棱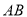 ,
, 中点,点
中点,点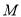 ,
,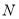 分别是线段
分别是线段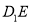 ,
,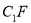 上的点,则与平面
上的点,则与平面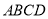 垂直的直线
垂直的直线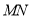 有( )条
有( )条
 是定义域为
是定义域为 的奇函数,那么
的奇函数,那么 .
.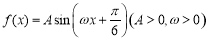 的图象在
的图象在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为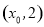 和
和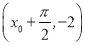 .
.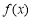 的解析式;
的解析式;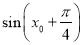 的值.
的值.