题目内容
已知函数![]() ,
,![]() 为函数
为函数![]() 的导函数.
的导函数.
(1)设函数f(x)的图象与x轴交点为A,曲线y=f(x)在A点处的切线方程是![]() ,求
,求![]() 的值;
的值;
(2)若函数![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
解:(Ⅰ)∵![]() ,
,
∴![]() .
.
∵![]() 在
在![]() 处切线方程为
处切线方程为![]() ,
,
∴![]() , ∴
, ∴![]() ,
,![]() .
.
(Ⅱ)![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
当![]() 时,
时,![]() ,
,
|
|
| 0 |
|
|
| - | 0 | + |
|
|
| 极小值 |
|
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
②当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() (ⅰ)当
(ⅰ)当![]() ,即
,即![]() 时,
时,
|
|
| 0 |
|
|
|
|
| - | 0 | + | 0 | - |
|
|
| 极小值 |
| 极大值 |
|
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() ;(ⅱ)当
;(ⅱ)当![]() ,即
,即![]() 时,
时,![]()
![]() , 故
, 故![]() 在
在![]() 单调递减;
单调递减;
(ⅲ)当![]() ,即
,即![]() 时,
时,
|
|
|
|
| 0 |
|
|
| - | 0 | + | 0 | - |
|
|
| 极小值 |
| 极大值 |
|
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递 综上所述,当
上单调递 综上所述,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
当![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ; 当
; 当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
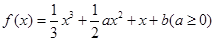 ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间. ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间. ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间.