题目内容
已知函数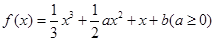 ,
, 为函数
为函数 的导函数.
的导函数.
(1)设函数f(x)的图象与x轴交点为A,曲线y=f(x)在A点处的切线方程是 ,求
,求 的值;
的值;
(2)若函数 ,求函数
,求函数 的单调区间.
的单调区间.
【答案】
(1)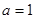 ,
,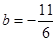 ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)先对原函数进行求导,易知点A坐标,又由曲线y=f(x)在A点处的切线方程是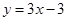 ,可得
,可得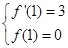 ,解得
,解得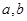 的值;(2)先写出
的值;(2)先写出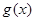 的函数解析式,再对函数
的函数解析式,再对函数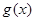 求导,然后对a分
求导,然后对a分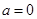 和
和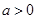 两种情况讨论,列表求单调区间.
两种情况讨论,列表求单调区间.
试题解析:(1)∵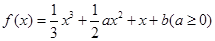 ,∴
,∴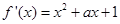 . 1分
. 1分
∵ 在
在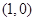 处切线方程为
处切线方程为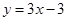 ,∴
,∴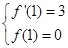 , 3分
, 3分
∴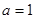 ,
,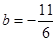 .
(各1分)
5分
.
(各1分)
5分
(2)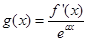
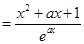
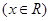 .
.
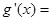
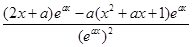
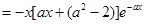 . 7分
. 7分
①当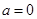 时,
时,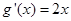 ,
,
|
|
|
0 |
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
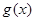 的单调递增区间为
的单调递增区间为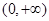 ,单调递减区间为
,单调递减区间为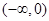 .
9分
.
9分
②当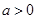 时,令
时,令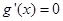 ,得
,得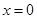 或
或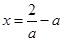 10分
10分
(ⅰ)当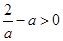 ,即
,即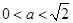 时,
时,
|
|
|
0 |
|
|
|
|
|
- |
0 |
+ |
0 |
- |
|
|
|
极小值 |
|
极大值 |
|
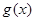 的单调递增区间为
的单调递增区间为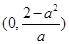 ,单调递减区间为
,单调递减区间为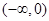 ,
,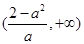 ; 11分
; 11分
(ⅱ)当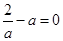 ,即
,即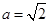 时,
时,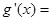
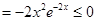 ,
故
,
故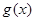 在
在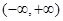 单调递减; 12分
单调递减; 12分
(ⅲ)当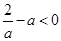 ,即
,即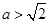 时,
时,
|
|
|
|
|
0 |
|
|
|
- |
0 |
+ |
0 |
- |
|
|
|
极小值 |
|
极大值 |
|
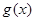 在
在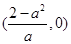 上单调递增,在
上单调递增,在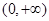 ,
,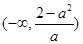 上单调递减
上单调递减
综上所述,当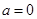 时,
时,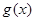 的单调递增区间为
的单调递增区间为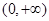 ,单调递减区间为
,单调递减区间为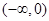 ;
;
当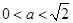 时,
时,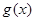 的单调递增区间为
的单调递增区间为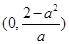 ,单调递减区间为
,单调递减区间为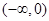 ;
;
当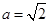 时,
时,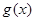 的单调递减区间为
的单调递减区间为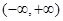 ;
;
当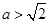 时,
时,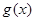 的单调递增区间为
的单调递增区间为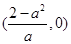 ,单调递减区间为
,单调递减区间为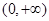 ,
,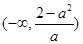 14分
14分
考点:1、导数性质的综合应用.2.函数的单调性.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目







 ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间. ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间.