题目内容
设函数f(x)定义在(0,+∞)上,f(1)=0,导函数![]()
(Ⅰ)求g(x)的单调区间和最小值;
(Ⅱ)讨论g(x)与![]() 的大小关系;
的大小关系;
(Ⅲ)是否存在x0>0,使得|g(x)-g(x0)|<![]() 对任意成立?若存在,求出x0的取值范围;若不存在,请说明理由.
对任意成立?若存在,求出x0的取值范围;若不存在,请说明理由.
答案:
解析:
解析:
|
解(Ⅰ)由题设易知 当 当 因此, (Ⅱ) 设 当 当 因此, 当 当 (Ⅲ)满足条件的x0不存在. 证明如下: 证法一:假设存在 即对任意x>0,有 但对上述x0,取 因此,不存在 证法二:假设存在 由(Ⅰ)知,g(x)的最小值为 又 ∴ 从而可取一个 即 ∴不存在 |

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
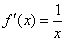 ,g(x)=f(x)+f′(x),
,g(x)=f(x)+f′(x), 的大小关系;
的大小关系;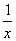 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由。
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由。