题目内容
设函数f(x)定义在(0,+∞)上,f(1)=0,导函数![]() ,
,![]() .
.
(1)求g(x)的单调区间和最小值;
(2)讨论g(x)与![]() 的大小关系;
的大小关系;
(3)是否存在x0>0,使得![]() 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.
答案:
解析:
解析:

(2)![]() ,设
,设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
因此函数![]() 在
在![]() 内单调递减,当
内单调递减,当![]() 时,
时,![]() =0,∴
=0,∴![]() ;
;
当![]() 时,
时,![]() =0,∴
=0,∴![]() .
.
(3)满足条件的![]() 不存在.证明如下:
不存在.证明如下:
证法一:假设存在![]() ,使
,使![]() 对任意
对任意![]() 成立,
成立,
即对任意![]() 有
有![]() ①
①
但对上述的![]() ,取
,取![]() 时,有
时,有![]() ,这与①左边的不等式矛盾,
,这与①左边的不等式矛盾,
因此不存在![]() ,使
,使![]() 对任意
对任意![]() 成立.
成立.
证法二:假设存在![]() ,使
,使![]() 对任意
对任意![]() 成立,
成立,


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
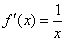 ,g(x)=f(x)+f′(x),
,g(x)=f(x)+f′(x), 的大小关系;
的大小关系;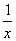 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由。
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由。