题目内容
设函数f(x)定义在(0,+∞)上,f(1)=0,导函数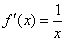 ,g(x)=f(x)+f′(x),
,g(x)=f(x)+f′(x),
(Ⅰ)求g(x)的单调区间和最小值;
(Ⅱ)讨论g(x)与 的大小关系;
的大小关系;
(Ⅲ)是否存在x0>0,使得|g(x)-g(x0)|<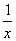 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由。
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由。
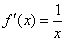 ,g(x)=f(x)+f′(x),
,g(x)=f(x)+f′(x),(Ⅰ)求g(x)的单调区间和最小值;
(Ⅱ)讨论g(x)与
 的大小关系;
的大小关系;(Ⅲ)是否存在x0>0,使得|g(x)-g(x0)|<
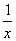 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由。
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由。 解:(Ⅰ)由题设易知f(x)=lnx,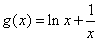 ,
,
∴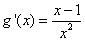 ,令g′(x)=0得x=1,
,令g′(x)=0得x=1,
当x∈(0,1)时,g′(x)<0,故(0,1)是g(x)的单调减区间;
当x∈(1,+∞)时,g′(x)>0,故(1,+∞)是g(x)的单调增区间,
因此,x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点,
所以最小值为g(1)=1。
(Ⅱ)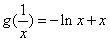 ,
,
设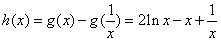 ,则
,则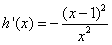 ,
,
当x=1时,h(1)=0,即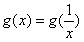 ,
,
当 时,
时,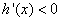 ,
,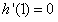 ,
,
因此,h(x)在(0,+∞)内单调递减;
当0<x<1时,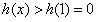 ,即
,即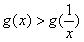 ;
;
当x>1时,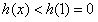 ,即
,即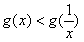 ;
;
(Ⅲ)满足条件的x0不存在;
证明如下:假设存在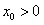 ,使
,使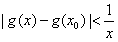 对任意x>0成立,
对任意x>0成立,
即对任意x>0,有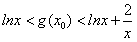 ,(*)
,(*)
但对上述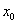 ,取
,取 时,有
时,有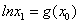 ,这与(*)左边不等式矛盾;
,这与(*)左边不等式矛盾;
因此,不存在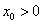 ,使
,使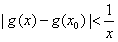 对任意x>0成立。
对任意x>0成立。
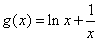 ,
,∴
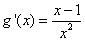 ,令g′(x)=0得x=1,
,令g′(x)=0得x=1,当x∈(0,1)时,g′(x)<0,故(0,1)是g(x)的单调减区间;
当x∈(1,+∞)时,g′(x)>0,故(1,+∞)是g(x)的单调增区间,
因此,x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点,
所以最小值为g(1)=1。
(Ⅱ)
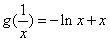 ,
,设
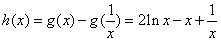 ,则
,则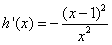 ,
,当x=1时,h(1)=0,即
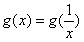 ,
,当
 时,
时,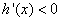 ,
,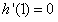 ,
,因此,h(x)在(0,+∞)内单调递减;
当0<x<1时,
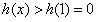 ,即
,即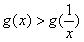 ;
;当x>1时,
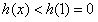 ,即
,即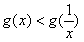 ;
;(Ⅲ)满足条件的x0不存在;
证明如下:假设存在
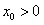 ,使
,使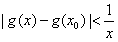 对任意x>0成立,
对任意x>0成立,即对任意x>0,有
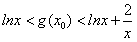 ,(*)
,(*)但对上述
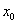 ,取
,取 时,有
时,有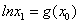 ,这与(*)左边不等式矛盾;
,这与(*)左边不等式矛盾;因此,不存在
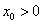 ,使
,使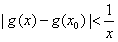 对任意x>0成立。
对任意x>0成立。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目