题目内容
已知函数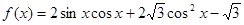 ,
,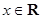 .
.
(1)求函数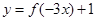 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)已知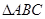 中的三个内角
中的三个内角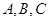 所对的边分别为
所对的边分别为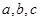 ,若锐角
,若锐角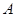 满足
满足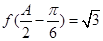 ,且
,且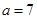 ,
,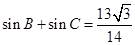 ,求
,求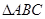 的面积.
的面积.
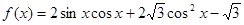 ,
,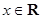 .
.(1)求函数
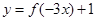 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;(2)已知
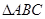 中的三个内角
中的三个内角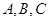 所对的边分别为
所对的边分别为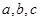 ,若锐角
,若锐角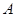 满足
满足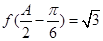 ,且
,且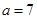 ,
,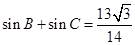 ,求
,求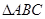 的面积.
的面积.(1) ;
; ,
, (2)
(2)
 ;
; ,
, (2)
(2)
试题分析:(1)利用二倍角公式先将
 降次,再利用辅助角公式,化成一个角的三角函数,然后求出
降次,再利用辅助角公式,化成一个角的三角函数,然后求出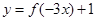 的解析式
的解析式 ,利用周期公式求出周期,令
,利用周期公式求出周期,令 ,解出
,解出 的范围就是
的范围就是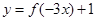 的等单调减区间;(2)由
的等单调减区间;(2)由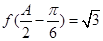 求出sinA,再利用正弦定理及条件
求出sinA,再利用正弦定理及条件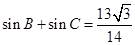 求出b+c,用余弦定理求出bc,再用三角形面积公式求出面积.
求出b+c,用余弦定理求出bc,再用三角形面积公式求出面积.试题解析:(1)




 的最小正周期为
的最小正周期为 3分
3分由
 得:
得: ,
, ,
,  的单调递减区间是
的单调递减区间是 ,
, 6分
6分(2)∵
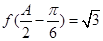 ,∴
,∴ ,∴
,∴ 7分
7分∵
 ,∴
,∴ .由正弦定理得:
.由正弦定理得: ,
,即
 ,∴
,∴ 9分
9分由余弦定理
 得:
得: ,
,即
 ,∴
,∴ 11分
11分∴
 12分
12分
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

 ,
,
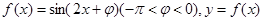 的图象的一条对称轴是直线
的图象的一条对称轴是直线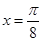 .
.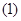 求
求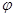 ;
;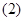 求函数
求函数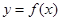 的单调增区间;
的单调增区间;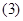 画出函数
画出函数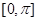 上的图象.
上的图象.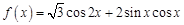 ,
,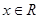 .
.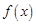 的最小正周期;
的最小正周期;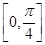 上的值域.
上的值域. 的最小正周期为
的最小正周期为 .
. 的对称轴方程;⑵设
的对称轴方程;⑵设 ,
, ,求
,求 的值.
的值.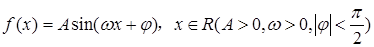 的一段图象如图5所示:将
的一段图象如图5所示:将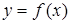 的图像向右平移
的图像向右平移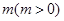 个单位,可得到函数
个单位,可得到函数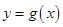 的图象,且图像关于原点对称,
的图象,且图像关于原点对称,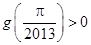 .
.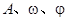 的值;
的值; 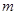 的最小值,并写出
的最小值,并写出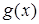 的表达式;
的表达式;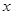 的函数
的函数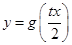 在区间
在区间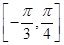 上最小值为
上最小值为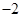 ,求实数
,求实数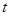 的取值范围.
的取值范围.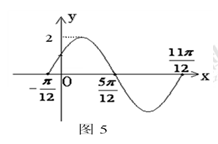
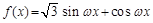 (ω>0)的图象与直线y=-2的两个相邻公共点之间的距离等于π,则
(ω>0)的图象与直线y=-2的两个相邻公共点之间的距离等于π,则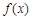 的单调递减区间是( )
的单调递减区间是( )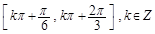
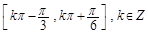
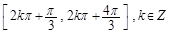
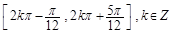
 , 则( ).
, 则( ). 两两为“同形”函数;
两两为“同形”函数; 为“同形”函数,且它们与
为“同形”函数,且它们与 不为“同形”函数;
不为“同形”函数; 为“同形”函数,且它们与
为“同形”函数,且它们与 不为“同形”函数.
不为“同形”函数. 的部分图象如图所示,则
的部分图象如图所示,则 ( )
( )