题目内容
【题目】如图,已知椭圆![]() 的长轴为
的长轴为![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴垂直,椭圆的离心率
轴垂直,椭圆的离心率![]() ,
, ![]() 为椭圆的左焦点,且
为椭圆的左焦点,且![]() .
.

(Ⅰ)求此椭圆的方程;
(Ⅱ)设![]() 是此椭圆上异于
是此椭圆上异于![]() 的任意一点,
的任意一点, ![]() ,
, ![]() 为垂足,延长
为垂足,延长![]() 到点
到点![]() 使得
使得![]() .连接
.连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,
, ![]() 为
为![]() 的中点,判定直线
的中点,判定直线![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 的位置关系.
的位置关系.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)由题意,根据条件列出关于![]() 的方程组,求解
的方程组,求解![]() 的值,再由
的值,再由![]() ,得到
,得到![]() 的值,即可求得椭圆的方程;
的值,即可求得椭圆的方程;
(Ⅱ)设![]() (
(![]() ),则
),则![]() ,因为点
,因为点![]() 坐标为
坐标为![]() ,得直线
,得直线![]() 的方程为
的方程为![]() ,进而得到
,进而得到![]() 坐标和
坐标和![]() 的直线方程,再利用圆心到直线的距离和圆的半径的关系,即可作出证明.
的直线方程,再利用圆心到直线的距离和圆的半径的关系,即可作出证明.
试题解析:
(Ⅰ)由题得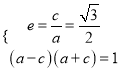 ,解得
,解得![]()
则![]()
则椭圆方程为![]()
(Ⅱ)![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 相切,证明如下:
相切,证明如下:
设![]() (
(![]() ),则
),则![]() 又因为点
又因为点![]() 坐标为
坐标为![]()
所以直线![]() 的斜率
的斜率![]()
则直线![]() 的方程为
的方程为![]() ,当
,当![]() 时,
时, ![]()
则![]() 点坐标为
点坐标为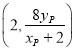 ,又因为
,又因为![]() ,则
,则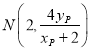
则直线![]() 的斜率为
的斜率为![]()
则直线![]() 的方程为:
的方程为: ![]()
则点![]() 到直线
到直线![]() 的距离为
的距离为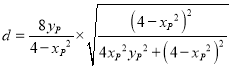
又因为![]()
则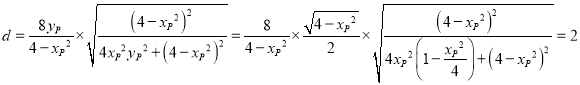
则![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 相切
相切

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
【题目】对某城市居民家庭年收入![]() (万元)和年“享受资料消费”
(万元)和年“享受资料消费”![]() (万元)进行统计分析,得数据如表所示.
(万元)进行统计分析,得数据如表所示.
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |
(1)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)若某家庭年收入为18万元,预测该家庭年“享受资料消费”为多少?
(参考公式: ,
,![]() )
)