题目内容
已知双曲线 上一点
上一点 ,过双曲线中心的直线交双曲线于
,过双曲线中心的直线交双曲线于 两点,记直线
两点,记直线 的斜率分别为
的斜率分别为 ,当
,当 最小时,双曲线离心率为( )
最小时,双曲线离心率为( )
A. B.
B. C
C D
D
B
解析试题分析:由题得,设点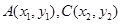 ,由于点A,B为过原点的直线与双曲线的焦点,所以根据双曲线的对称性可得A,B关于原点对称,即
,由于点A,B为过原点的直线与双曲线的焦点,所以根据双曲线的对称性可得A,B关于原点对称,即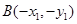 .则
.则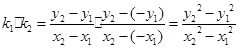 ,由于点A,C都在双曲线上,故有
,由于点A,C都在双曲线上,故有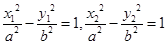 ,两式相减得
,两式相减得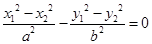
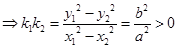 .则
.则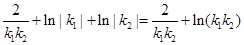 ,对于函数
,对于函数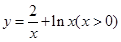 利用导数法可以得到当
利用导数法可以得到当 时,函数
时,函数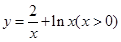 取得最小值.故当
取得最小值.故当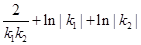 取得最小值时,
取得最小值时, 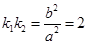 ,所以
,所以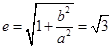 ,故选B
,故选B
考点:导数 最值 双曲线 离心率

练习册系列答案
相关题目
已知椭圆
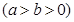 的离心率
的离心率 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根
的两个实根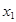 ,
,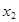 ,则点
,则点 ( )
( )
A.必在圆 内 内 | B.必在圆 上 上 |
C.必在圆 外 外 | D.以上三种情况都有可能 |
若 ,则方程
,则方程 表示( )
表示( )
A.焦点在 轴上的椭圆 轴上的椭圆 | B.焦点在 轴上的椭圆 轴上的椭圆 |
C.焦点在 轴上的双曲线 轴上的双曲线 | D.焦点在 轴上的双曲线 轴上的双曲线 |
直线 交双曲线
交双曲线 于
于 两点,
两点, 为双曲线
为双曲线 上异于
上异于 的任意一点,则直线
的任意一点,则直线 的斜率之积为( )
的斜率之积为( )
A. | B. | C. | D. |
已知抛物线 上一点P到y轴的距离为6,则点P到焦点的距离为( )
上一点P到y轴的距离为6,则点P到焦点的距离为( )
| A.7 | B.8 | C.9 | D.10 |
已知双曲线 的顶点恰好是椭圆
的顶点恰好是椭圆 的两个顶点,且焦距是
的两个顶点,且焦距是 ,则此双曲线的渐近线方程是( )
,则此双曲线的渐近线方程是( )
A. | B. | C. | D. |
已知抛物线 与双曲线
与双曲线 有相同的焦点F,点A是两曲线的一个交点,且
有相同的焦点F,点A是两曲线的一个交点,且 轴,则双曲线的离心率为( )
轴,则双曲线的离心率为( )
| A.2 | B. | C. | D. |
已知双曲线C1: =1(a>0,b>0)的离心率为2,若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( ).
=1(a>0,b>0)的离心率为2,若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( ).
A.x2= y y | B.x2= y y |
| C.x2=8y | D.x2=16y |

 ,左右焦点分别为
,左右焦点分别为 ,
, ,过
,过 两点,若
两点,若 的最大值为8,则
的最大值为8,则 的值是( )
的值是( )


