题目内容
直线 交双曲线
交双曲线 于
于 两点,
两点, 为双曲线
为双曲线 上异于
上异于 的任意一点,则直线
的任意一点,则直线 的斜率之积为( )
的斜率之积为( )
A. | B. | C. | D. |
B
解析试题分析:本题考查直线与圆锥曲线的相交问题,作为选择题尽量不要小题大做,所以可用特值法:令k=0,则A(-2,0)、B(2,0),,取P(4,3),可得
 .
.
考点:直线与圆锥曲线相交.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知 ,
, ,
, ,则动点
,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 | C.抛物线 | D.双曲线 |
已知点 是抛物线
是抛物线 的焦点,点
的焦点,点 在该抛物线上,且点
在该抛物线上,且点 的横坐标是
的横坐标是 ,则
,则 =( )
=( )
| A.2 | B.3 | C.4 | D.5 |
双曲线 的渐近线与抛物线
的渐近线与抛物线 相切,则该双曲线的离心率等于( )
相切,则该双曲线的离心率等于( )
A.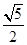 | B. | C. | D. |
若曲线 为焦点在
为焦点在 轴上的椭圆,则实数
轴上的椭圆,则实数 ,
,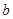 满足( )
满足( )
A. | B.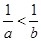 | C. | D. |
已知抛物线y2=2px(p>0),过其焦点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为 ( ).
| A.x=1 | B.x=-1 | C.x=2 | D.x=-2 |
 :
:
 的焦点与双曲线
的焦点与双曲线 :
: 的左焦点的连线交
的左焦点的连线交 .若
.若 ( )
( )



 上一点
上一点 ,过双曲线中心的直线交双曲线于
,过双曲线中心的直线交双曲线于 两点,记直线
两点,记直线 的斜率分别为
的斜率分别为 ,当
,当 最小时,双曲线离心率为( )
最小时,双曲线离心率为( ) B.
B. C
C D
D
 =1的左、右焦点分别为F1,F2,M是椭圆上一点,N是MF1的中点,若|ON|=1,则|MF1|等于( ).
=1的左、右焦点分别为F1,F2,M是椭圆上一点,N是MF1的中点,若|ON|=1,则|MF1|等于( ).