题目内容
设函数f(x)=x2-2|x|-1(-3≤x≤3).
(1)证明f(x)是偶函数;
(2)指出函数f(x)的单调区间,并说明在各个单调区间上f(x)是增函数还是减函数;
(3)求函数的值域.
[解析] (1)证明:∵定义域关于原点对称,
f(-x)=(-x)2-2|-x|-1=x2-2|x|-1=f(x),
即f(-x)=f(x),∴f(x)是偶函数.
(2)当x≥0时,f(x)=x2-2x-1=(x-1)2-2,
当x<0时,f(x)=x2+2x-1=(x+1)2-2,
即f(x)=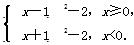
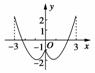
根据二次函数的作图方法,可得函数图像,如图
函数f(x)的单调区间为[-3,-1),[-1,0),[0,1),[1,3].
f(x)在区间[-3,-1),[0,1]上为减函数,
在[-1,0),[1,3]上为增函数.
(3)当x≥0时,函数f(x)=(x-1)2-2的最小值为-2,最大值为f(3)=2.
当x<0时,函数f(x)=(x+1)2-2的最小值为-2,最大值为f(-3)=2.
故函数f(x)的值域为[-2,2].

练习册系列答案
相关题目
 的定义域为________.
的定义域为________.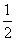 ,
,
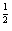 D.f(x)=(
D.f(x)=(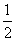 )x
)x +tan
+tan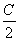 +
+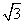 tan
tan