题目内容
1.若x1,x2,…,x2017的平均数为4,标准差为3,且yi=-3(xi-2),i=x1,x2,…,x2017,则新数据y1,y2,…,y2017的平均数和标准差分别为( )| A. | -6 9 | B. | -6 27 | C. | -12 9 | D. | -12 27 |
分析 利用平均数及标准差的定义与性质即可求解.
解答 解:x1,x2,…,x2017的平均数为$\overline{x}$=4,标准差为s=3,
且yi=-3(xi-2),i=x1,x2,…,x2017,
∴新数据y1,y2,…,y2017的平均数是$\overline{y}$=-3($\overline{x}$-2)=-3×(4-2)=-6;
方差为(-3)2•s2=9×32=81,标准差为$\sqrt{81}$=9;
综上,新数据的平均数和标准差分别为-6和9.
故选:A.
点评 本题考查了平均数和标准差的求法与应用问题,是基础题.

练习册系列答案
相关题目
9.为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如表:
某校研究性学习小组,从汽车市场上随机选取了M辆纯电动乘用车,根据其续驶里程R(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(1)求x、y、z、M的值;
(2)若从这M辆纯电动乘用车任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为X(单位:万元),求X的分布列和数学期望值E(X).
| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程R(公里) | ||
| 100≤R<180 | 180≤R<280 | <280 | |
| 纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
| 分组 | 频数 | 频率 |
| 100≤R<180 | 3 | 0.3 |
| 180≤R<280 | 6 | x |
| R≥280 | y | z |
| 合计 | M | 1 |
(2)若从这M辆纯电动乘用车任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为X(单位:万元),求X的分布列和数学期望值E(X).
10.设i是虚数单位,若复数$a+\frac{2i}{1-i}$(a∈R)是纯虚数,则a=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
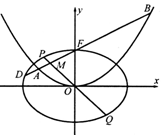 如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.
如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.