题目内容
选修4—1:几何证明选讲
如图, 内接于⊙
内接于⊙ ,
,  是⊙
是⊙ 的直径,
的直径,  是过点
是过点 的直线, 且
的直线, 且 .
.

(Ⅰ)求证:  是⊙
是⊙ 的切线;
的切线;
(Ⅱ)如果弦 交
交 于点
于点 ,
,  ,
,  ,
,  , 求
, 求 .
.
(Ⅰ)证明见解析;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)根据直径所对的圆周角为直角,所以 与
与 互余,又因为:
互余,又因为: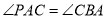 所以:
所以: 与
与 互余,所以
互余,所以 是
是 的切线;(Ⅱ)根据题意中的比例关系及相交弦定理
的切线;(Ⅱ)根据题意中的比例关系及相交弦定理 可求得:
可求得: ,又因为等弦所对的圆周角相等,所以角
,又因为等弦所对的圆周角相等,所以角 等于角
等于角 ,又因为
,又因为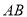 是直径,所以角
是直径,所以角 为直角,
为直角, ,进而求得
,进而求得 .
.
试题解析:(Ⅰ)证明: 为直径,
为直径,
 ,
,
 为直径,
为直径,
 为圆的切线
为圆的切线 4分
4分
(Ⅱ)

 ∽
∽

 ∽
∽


 在直角三角形
在直角三角形 中
中

 10分
10分
考点:1.直径所对的圆周角为直角;2.三角形相似及相交弦定理.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
2014年一轮又一轮的寒潮席卷全国.某商场为了了解某品牌羽绒服的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气
温,数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程=bx+a中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月羽绒服的销售量约为________件.
 的终边经过点
的终边经过点 ,且
,且 ,则
,则 的值为
的值为 
 (B)
(B) (C)
(C) (D)
(D)
 中,
中, 是AB中点,且对于边AB上任一点P,恒有
是AB中点,且对于边AB上任一点P,恒有 ,则有
,则有 B.
B.  C.
C.  D.
D. 
 ”是“函数
”是“函数 在区间
在区间 上为减函数”的
上为减函数”的 的面积
的面积 满足
满足 ,且
,且 .
. 的取值范围;
的取值范围; ,求
,求 的最大值.
的最大值.
 满足
满足 则下列不等式一定成立的是( )
则下列不等式一定成立的是( ) B.
B. C.
C. D.
D.
 ,若存在实数
,若存在实数 ,满足
,满足 ,其中
,其中 ,则
,则 取值范围是 .
取值范围是 .