题目内容
已知a=(2,1),b=(-1,3),c=(1,2),求p=2a+3b-4c,并以{a,b}为基底来表示p.
解:p=2(2,1)+3(-1,3)-4(1,2)
=(-3,3).
由平面向量基本定理知,存在实数λ,μ使p=λa+μb.
∴(-3,3)=λ(2,1)+μ(-1,3).
即(-3,3)=(2λ-μ,λ+3μ),
∴![]() 解得
解得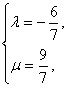
∴p=-![]() a+
a+![]() b.
b.

练习册系列答案
相关题目
题目内容
已知a=(2,1),b=(-1,3),c=(1,2),求p=2a+3b-4c,并以{a,b}为基底来表示p.
解:p=2(2,1)+3(-1,3)-4(1,2)
=(-3,3).
由平面向量基本定理知,存在实数λ,μ使p=λa+μb.
∴(-3,3)=λ(2,1)+μ(-1,3).
即(-3,3)=(2λ-μ,λ+3μ),
∴![]() 解得
解得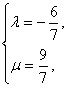
∴p=-![]() a+
a+![]() b.
b.
