题目内容
19.已知在△ABC中,角A,B,C的对边分别为a,b,c,若A=120°,a=3$\sqrt{3}$(1)求bc的最大值;
(2)若D为BC边上靠近点B的一个三等分点,求AD的取值范围.
分析 (1)由余弦定理可得:$(3\sqrt{3})^{2}$=b2+c2-2bccos120°≥2bc+bc,解得bc即可.
(2)如图所示,以BC所在直线为x轴,线段BC的垂直平分线为y轴建立直角坐标系.D$(-\frac{1}{2}\sqrt{3},0)$.∠BAC=120°,可得∠OEC=60°.E$(0,-\frac{3}{2})$,EC=3.点A所在圆的方程为:x2+$(y+\frac{3}{2})^{2}$=9,$(-\frac{3}{2}\sqrt{3}<x<\frac{3\sqrt{3}}{2},0<y≤\frac{3}{2})$.可设设x=3cosθ,y=-$\frac{3}{2}$+3sinθ,$\frac{π}{6}<θ<\frac{5π}{6}$,$sin(θ-\frac{π}{6})$∈(0,1].代入|AD|2=$(x+\frac{\sqrt{3}}{2})^{2}+{y}^{2}$,化简整理即可得出.
解答  解:(1)由余弦定理可得:$(3\sqrt{3})^{2}$=b2+c2-2bccos120°≥2bc+bc,解得bc≤9,当且仅当b=c=3时取等号,
解:(1)由余弦定理可得:$(3\sqrt{3})^{2}$=b2+c2-2bccos120°≥2bc+bc,解得bc≤9,当且仅当b=c=3时取等号,
∴bc的最大值为9
(2)如图所示,以BC所在直线为x轴,线段BC的垂直平分线为y轴建立直角坐标系.D$(-\frac{1}{2}\sqrt{3},0)$.
∵∠BAC=120°,可得∠OEC=60°.
∴E$(0,-\frac{3}{2})$,EC=3.
∴点A所在圆的方程为:x2+$(y+\frac{3}{2})^{2}$=9,$(-\frac{3}{2}\sqrt{3}<x<\frac{3\sqrt{3}}{2},0<y≤\frac{3}{2})$.
可设设x=3cosθ,y=-$\frac{3}{2}$+3sinθ,$\frac{π}{6}<θ<\frac{5π}{6}$,$sin(θ-\frac{π}{6})$∈(0,1].
∴|AD|2=$(x+\frac{\sqrt{3}}{2})^{2}+{y}^{2}$=$(3cosθ+\frac{\sqrt{3}}{2})^{2}$+$(-\frac{3}{2}+3sinθ)^{2}$
=-$6\sqrt{3}$$sin(θ-\frac{π}{6})$+12∈$(12-6\sqrt{3},12]$,
∴|AD|∈$(3-\sqrt{3},2\sqrt{3}]$.
点评 本题考查了余弦定理、基本不等式的性质、圆的方程及其应用、三角函数求值、和差化积,考查了推理能力与计算能力,属于中档题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
| A. | 若a<1,b<$\frac{1}{2}$,则a>b | B. | 若a<1,b<$\frac{1}{2}$,则a<b | ||
| C. | 若a>1,b>$\frac{1}{2}$,则a>b | D. | 若a>1,b>$\frac{1}{2}$,则a<b |
 如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,M为PC的中点.
如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,M为PC的中点. 如图,在四边形ABCD中,CB=CA=$\frac{1}{2}$AD=1,$\overrightarrow{CA}•\overrightarrow{AD}$=-1,sin∠BCD=$\frac{3}{5}$.
如图,在四边形ABCD中,CB=CA=$\frac{1}{2}$AD=1,$\overrightarrow{CA}•\overrightarrow{AD}$=-1,sin∠BCD=$\frac{3}{5}$.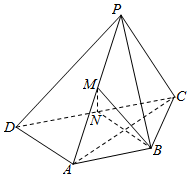 如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.
如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.