题目内容
11.已知集合A={x|y=lnx},B={x|x2-2x-3<0},则A∩B=( )| A. | (0,3) | B. | (-∞,-1)∪(0,+∞) | C. | (-∞,-1)∪(3,+∞) | D. | (-1,3) |
分析 求出A中x的范围确定出A,求出B中不等式的解集确定出B,找出A与B的交集即可.
解答 解:由A中y=lnx,得到x>0,即A=(0,+∞),
由B中不等式变形得:(x-3)(x+1)<0,
解得:-1<x<3,即B=(-1,3),
则A∩B=(0,3),
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
20.有3个大学毕业生,现在有两个工作岗位可选择,共有( )种选法.
| A. | 9 | B. | 8 | C. | 6 | D. | 5 |
17.关于函数f(x)=|tanx|的性质,下列叙述不正确的是( )
| A. | f(x)的最小正周期为$\frac{π}{2}$ | |
| B. | f(x)是偶函数 | |
| C. | f(x)的图象关于直线x=$\frac{kπ}{2}$(k∈Z)对称 | |
| D. | f(x)在每一个区间(kπ,kπ+$\frac{π}{2}$)(k∈Z)内单调递增 |
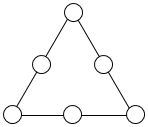 如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3 中的一个.
如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3 中的一个. 我国的人口呈现老龄化趋势,某城市为提高老年人的养老服务质量,分别从甲、乙两个社区随机抽取了7名70岁以上的老年人进行走访,这14名老年人的年龄如图的茎叶图所示,其中甲社区7人的平均年龄为85岁.
我国的人口呈现老龄化趋势,某城市为提高老年人的养老服务质量,分别从甲、乙两个社区随机抽取了7名70岁以上的老年人进行走访,这14名老年人的年龄如图的茎叶图所示,其中甲社区7人的平均年龄为85岁.