题目内容
若数列{an},{bn}的通项公式分别是an=(-1)n+2 013·a,bn=2+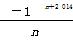 ,且an<bn对任意n∈N*恒成立,则常数a的取值范围是( )
,且an<bn对任意n∈N*恒成立,则常数a的取值范围是( )
A.(-2,1) B.[-2,1)
C.(-2,1] D.[-2,1]
解:(1)由an= ,可得an-an-1=
,可得an-an-1= ,n∈N*,n≥2.所以{an}是等差数列.
,n∈N*,n≥2.所以{an}是等差数列.
又因为a1=1,
所以an=1+(n-1)× =
= ,n∈N*.
,n∈N*.
 令p=2n+3,则p≥5,p∈N*.
令p=2n+3,则p≥5,p∈N*.
g(n)=p+ -6(n∈N*),易知p=5时,g(n)min=
-6(n∈N*),易知p=5时,g(n)min= .所以t≤
.所以t≤ ,即实数t的取值范围是
,即实数t的取值范围是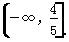

练习册系列答案
相关题目
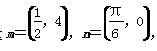 ,点P在y=cos x的图象上运动,点Q在y=f(x)的图象上运动,且满足
,点P在y=cos x的图象上运动,点Q在y=f(x)的图象上运动,且满足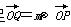 +n(其中O为坐标原点),则y=f(x)在区间
+n(其中O为坐标原点),则y=f(x)在区间 上的最大值是( )
上的最大值是( )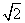 D.2
D.2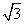
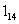 01)2转换成十进制数是( )
01)2转换成十进制数是( )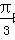 时取得最小值-4.
时取得最小值-4.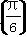 ,求数列
,求数列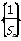 的前n项和Tn.
的前n项和Tn.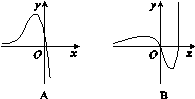
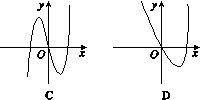
 且x+y=1,函数f(m)=
且x+y=1,函数f(m)=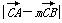 的最小值为
的最小值为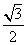 ,则
,则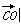 的最小值为________
的最小值为________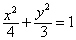 的离心率为 ( )
的离心率为 ( )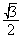 B.
B.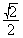 C.
C. D.
D.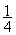
 ,直线
,直线 ,则
,则 与
与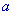 的位置关系是( )
的位置关系是( )