对于实数a＞0且a≠1.函数f(x)=loga(x-1)+3的图象恒过定点P.则定点P的坐标是(2.3)．题目和参考答案——青夏教育精英家教网—

题目内容

11．对于实数a＞0且a≠1，函数f（x）=log_a（x-1）+3的图象恒过定点P，则定点P的坐标是（2，3）．

分析由对数函数的性质可得f（2）=3，可得定点．

解答解：由对数的性质y=log_ax，恒过（1，0），即log_a1=0，
∴令x-1=1可得x=2，
∴f（2）=log_a（2-1）+3=3，
∴函数图象恒过定点（2，3），
故答案为：（2，3）．

点评本题考查对数函数恒过定点问题，属基础题．

练习册系列答案

2．已知圆C：x²+y²-8y+12=0，直线l：ax+y+2a=0
（1）当直线l与圆C相切时，求a的值；
（2）当a=-1时，直线l与圆C相交于A，B两点，求|AB|．

19．

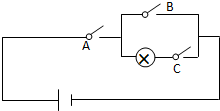如图所示电路，有A、B、C三个开关，每个开关开或关的概率都是$\frac{1}{2}$，且相互独立，则灯泡亮的概率（　　）

6．若正数a，b满足a+b=10，则$\sqrt{a+2}$+$\sqrt{b+3}$的最大值为$\sqrt{30}$．

16．

如图，在四棱锥 P-ABCD中，底面 ABCD为矩形，PA⊥平面ABCD，点 E在线段 PC上，PC⊥平面 BDE．
（1）求证：BD⊥平面 PAC；
（2）若 PA=1，AD=2，求二面角 B-PC-A的大小．

3．下列函数中，在区间（0，+∞）上是减函数的是（　　）

20．已知函数f（x）=$\frac{1}{3}$x³+$\frac{4}{3}$．求过点P（2，4）的函数f（x）的切线方程．

1．已知函数f（x）=xe^x，其中e是自然对数的底数，若存在整数t使方程f（x）=x+2在[t，t+1]上有解，则满足条件的所有整数t的取值集合为{-3，1}．

试题分类