题目内容
已知直线l被两直线l1:4x+y+6=0和l2:3x-5y-6=0截得线段的中点为P(0,0),求直线l的方程.
考点:中点坐标公式,两条直线的交点坐标
专题:直线与圆
分析:设所求直线l与两直线l1,l2分别交于A(x1,y1),B(x2,y2),则x1+x2=0,且y1+y2=0,由点A(x1,y1),B(x2,y2)分别在直线l1,l2上,解得
,由此能求出直线l的方程.
|
解答:
解:设所求直线l与两直线l1,l2分别交于A(x1,y1),B(x2,y2),
则x1+x2=0,且y1+y2=0,…4分
又因为点A(x1,y1),B(x2,y2)分别在直线l1,l2上,
则
,
即
,
解得
,
所求直线l即为直线AP,
所以y=-
x为所求.…10分.
则x1+x2=0,且y1+y2=0,…4分
又因为点A(x1,y1),B(x2,y2)分别在直线l1,l2上,
则
|
即
|
解得
|
所求直线l即为直线AP,
所以y=-
| 1 |
| 6 |
点评:本题考查直线方程的求法,是基础题,解题时要认真审题,注意中点坐标公式的合理运用.

练习册系列答案
相关题目
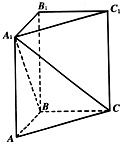 在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,BB1=2,求:
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,BB1=2,求: