题目内容
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称函数f(x)为M上的l高调函数.现给出下列命题:
①函数f(x)=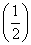 x是R上的1高调函数;
x是R上的1高调函数;
②函数f(x)=sin 2x为R上的π高调函数;
③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是[2,+∞).
其中正确的命题是________.(写出所有正确命题的序号)
②③解析: 对于①,∵x∈R,∴x+1∈R.
又f(x)=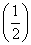 x在R上是减函数,
x在R上是减函数,
∴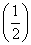 x+1<
x+1<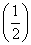 x,即f(x+1)<f(x).
x,即f(x+1)<f(x).
∴①错.
对于②,∵x∈R,∴x+π∈R.
∴f(x+π)=sin 2(x+π)=sin 2x=f(x).
∴②正确.
对于③ ,∵f(x)=x2为[-1,+∞)上的m高调函数,
∴f(x+m)≥f(x)即(x+m)2≥x2,
∴2mx+m2≥0对于x∈[-1,+∞)恒成立.
∴ .
.
∴m≥2,即③正确.
∴正确命题是②,③.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目

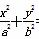 =1(a>b>0)的面积S=πab
=1(a>b>0)的面积S=πab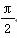
 D.θ=
D.θ=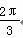
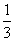 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.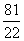 B.
B.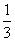
 的一个特征值为2,其对应的一个特征向量为α=
的一个特征值为2,其对应的一个特征向量为α= .
. ,求x,y的值.
,求x,y的值.