题目内容
设函数f(x)＝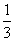
x3－ax2－ax，g(x)＝2x2＋4x＋c.
(1)试问函数f(x)能否在x＝－1时取得极值？说明理由；
(2)若a＝－1，当x∈[－3,4]时，函数f(x)与g(x)的图象有两个公共点，求c的取值范围．
解析： (1)由题意f′(x)＝x2－2ax－a，
假设在x＝－1时f(x)取得极值，则有f′(－1)＝(－1)2－2a(－1)－a＝0，解得a＝－1.
而此时f′(x)＝x2＋2x＋1＝(x＋1)2≥0，所以函数f(x)在R上为增函数，函数无极值．
这与f(x)在x＝－1处有极值矛盾，所以f(x)在x＝－1处无极值．
(2)设f(x)＝g(x)，则有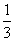x3－ax2－ax＝2x2＋4x＋c，
所以c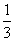＝x3－x2－3x.
设F(x)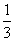＝x3－x2－3x，则F′(x)＝x2－2x－3，令F′(x)＝0，解得x1＝－1，x2＝3.
当x变化时，F′(x)，F(x)的变化情况如表所示：
| x | －3 | (－3，－1) | －1 | (－1,3) | 3 | (3,4) | 4 |
| F′(x) |
| ＋ | 0 | － | 0 | ＋ | |
| F(x) | －9 | 极大值 | 极小值 | － |
练习册系列答案
阅读快车系列答案
相关题目
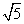，C是圆O外一点，AC交圆O于点E，BC交圆O于点D，已知AC＝AB，BC＝4，求△ADE的周长．
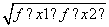＝C，则称函数f(x)在D上的几何平均数为C.已知f(x)＝x3，x∈[1,2]，则函数f(x)＝x3在[1,2]上的几何平均数为( )
B．2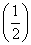
x是R上的1高调函数；
B. 
D. 
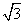，若其中一个圆的半径为4，则另一个圆的半径为( )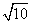
D．2